Huomioita ryhmästä

Määritelmä. Ryhmän (G,*) alkioiden lukumäärää G sanotaan ryhmän kertaluvuksi.

Jos G = n, jollekin positiiviselle kokonaisluvulle n, sanotaan, että ryhmä (G,*) on äärellinen ryhmä. Muussa tapauksessa ryhmä on ääretön.

Määritellään lyhennysmerkintä aⁿ yhden alkion usealle peräkkäiselle operaatiolle

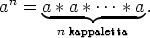
Merkitään a^-n = (a^-1)ⁿ positiiviselle kokonaisluvulle n ja a⁰ = e, missä e on ryhmän neutraalialkio. Osoitetaan, että tavalliset potenssin laskusäännöt pätevät tälle määrittelylle, toisin sanoen (aⁿ)^m = a^nm ja aⁿ * a^m = a^n+m kaikille kokonaisluvuille n ja m. Mikäli n ja m ovat ei-negatiivisia kokonaislukuja on yhtälöiden toteutuminen selvää. Oletetaan, että n ja m ovat positiivisia kokonaislukuja. Silloin (a^-n)^m = ((a^-1)ⁿ)^m = (a^-1)^nm = a^-nm. Soveltamalla sivun Ryhmän perusominaisuuksia lauseen kohtaa (iv) toistuvasti nähdään, että (aⁿ)^-1 = (a^-1)ⁿ = a^-n. Täten (aⁿ)^-m = ((aⁿ)^-1)^m = (a^-n)^m = a^-nm. Vielä (a^-n)^-m = ((a^-n)^-1)^m = (aⁿ)^m = a^nm. Toinen yhtälö negatiivisille potensseille voidaan todistaa seuraavasti: a^-n * a^m = (a^-1)ⁿ * a^m = a^-n+m. Samoin aⁿ * a^-m = a^n-m. Lopuksi a^-n * a^-m = (a^-1)ⁿ * (a^-1)^m = (a^-1)^n+m = a^-n-m.

Huomaa, että potenssilaskun tuttua sääntä (ab)ⁿ = aⁿbⁿ ei voida yleistää ryhmän alkioille.

Jos G on ryhmä yhteenlaskun + suhteen, niin ylläoleva merkintä aⁿ kirjoitetaan muotoon na.

Ryhmästä (G, ^. ), jossa laskutoimitus on kertolasku, voidaan käyttää nimitystä multiplikatiivinen ryhmä. Vastaavasti ryhmästä (G, +), jonka laskutoimitus on yhteenlasku, voidaan käyttää nimitystä additiivinen ryhmä.

Additiivisessa ryhmässä alkion a käänteisalkiosta -a voidaan käyttää myös nimitystä vasta-alkio. Jos ryhmän (G,*) neutraalialkio on 0, voidaan puhua nolla-alkiosta ja vastaavasti, jos neutraalialkio on 1, voidaan puhua ykkösalkiosta.

Linkit:
Ryhmä
Ryhmän perusominaisuuksia
Esimerkkejä ryhmistä 2