| Sanna Ranto, LUKUTEORIA JA ALGEBRA Versio 1, 1.11.2003 | RYHMÄ |
Esimerkkejä ryhmistä 2
Esimerkki.(VEKTORIRYHMÄT) Vektoriavaruuden (V, +, . ) vektorit muodostavat
additiivisen Abelin ryhmän. Tämän ryhmän neutraalialkio on nollavektori  ja vektorin
X käänteisalkio on vastavektori -X. Tällaisen ryhmän muodostaa esimerkiksi
ja vektorin
X käänteisalkio on vastavektori -X. Tällaisen ryhmän muodostaa esimerkiksi
 n = {(a
1,...,an) | ai
n = {(a
1,...,an) | ai 
 , 1 < i < n}.
, 1 < i < n}.
Esimerkki.(MATRIISIRYHMÄT) Reaalilukualkioisten (m × n)-matriisien joukko Mm×n( )
muodostaa additiivisen Abelin ryhmän matriisien yhteenlaskun suhteen. Ryhmän
neutraalialkiona on nollamatriisi ja matriisin A käänteisalkiona on -A. (Tämä ryhmä kuuluu
itse asiassa jo edellisen esimerkin piiriin.)
)
muodostaa additiivisen Abelin ryhmän matriisien yhteenlaskun suhteen. Ryhmän
neutraalialkiona on nollamatriisi ja matriisin A käänteisalkiona on -A. (Tämä ryhmä kuuluu
itse asiassa jo edellisen esimerkin piiriin.)
Säännöllisten (n × n)-matriisien joukko

muodostaa multiplikatiivisen ryhmän matriisitulon suhteen. Ryhmän neutraalialkio on
identiteettimatriisi In ja matriisin A käänteisalkio on käänteismatriisi A-1. Kun n > 1, ryhmä
(GLn( ), . ) on esimerkki ryhmästä, joka ei ole Abelin ryhmä.
), . ) on esimerkki ryhmästä, joka ei ole Abelin ryhmä.
Esimerkki.(JÄÄNNÖSLUOKKARYHMÄT) Jäännösluokat modulo m muodostavat Abelin
ryhmän ( m, +), kun yhteenlasku määritellään seuraavasti
m, +), kun yhteenlasku määritellään seuraavasti  +
+  =
= 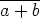 . Ryhmän
neutraalialkio on jäännösluokka
. Ryhmän
neutraalialkio on jäännösluokka  ja jäännösluokan
ja jäännösluokan  käänteisalkio on jäännösluokka
käänteisalkio on jäännösluokka  .
Ryhmä (
.
Ryhmä ( m, +) on esimerkki äärellisestä ryhmästä, sillä
m, +) on esimerkki äärellisestä ryhmästä, sillä 
 m = m.
m = m.
Jäännösluokkaa  modulo m sanotaan alkuluokaksi, jos syt(a,m) = 1. Tämä käsite on hyvin
määritelty, sillä
modulo m sanotaan alkuluokaksi, jos syt(a,m) = 1. Tämä käsite on hyvin
määritelty, sillä

Todistetaan tämä. Koska  =
= 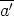 , niin a = a' + mk jollekin kokonaisluvulle k. Koska
syt(a,m) = 1, on olemassa sellaiset luvut u ja v, että 1 = ua + vm. Yhdistämällä nämä saadaan
1 = ua + vm = u(a' + mk) + vm = ua' + (uk + v)m. Koska luku 1 voidaan esittää lukujen a' ja
m monikertojen summana, on syt(a',m) = 1.
, niin a = a' + mk jollekin kokonaisluvulle k. Koska
syt(a,m) = 1, on olemassa sellaiset luvut u ja v, että 1 = ua + vm. Yhdistämällä nämä saadaan
1 = ua + vm = u(a' + mk) + vm = ua' + (uk + v)m. Koska luku 1 voidaan esittää lukujen a' ja
m monikertojen summana, on syt(a',m) = 1.
Kaikkien alkuluokkien modulo m joukko
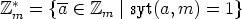
muodostaa ryhmän jäännösluokkien kertolaskun  .
.  =
=  suhteen. Ryhmän neutraalialkio
on jäännösluokka
suhteen. Ryhmän neutraalialkio
on jäännösluokka  . Alkuluokan
. Alkuluokan  käänteisalkio on se jäännösluokka, joka toteuttaa
kongruenssin
käänteisalkio on se jäännösluokka, joka toteuttaa
kongruenssin

silloinhan 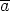 .
.  =
=  =
=  . Kuten Diofantoksen yhtälöiden kohdalla todetaan, tällä
kongruenssilla on yksikäsitteinen ratkaisu x välillä 0 < x < m - 1.
. Kuten Diofantoksen yhtälöiden kohdalla todetaan, tällä
kongruenssilla on yksikäsitteinen ratkaisu x välillä 0 < x < m - 1.
Esimerkiksi 
 = {
= { ,
,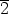 ,
, ,
,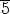 ,
,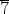 ,
, }.
}.
Linkit:
Ryhmä
Vektoriavaruus
Matriisi
Yksinkertaisia matriiseja
Säännöllinen matriisi
Jäännösluokka
Suurin yhteinen tekijä
Diofantoksen yhtälö