| Sanna Ranto, LUKUTEORIA JA ALGEBRA Versio 1, 1.11.2003 | LUKUTEORIA |
Jäännösluokka
Kongruenssi modulo m hajottaa joukon  ekvivalenssiluokkiin, jotka ovat muotoa:
ekvivalenssiluokkiin, jotka ovat muotoa:
![[a] = {a + mk | k (- Z}.](images/smr0100x.gif)
Ekvivalenssiluokkaa [a] sanotaan luvun a jäännösluokaksi modulo m. Jäännösluokasta käytetään
yleensä merkintää  tai a + m
tai a + m . Samassa jäännösluokassa olevat luvut antavat saman
jakojäännöksen luvulla m jaettaessa. Kaikkien jäännösluokkien modulo m joukosta käytetään
merkintää
. Samassa jäännösluokassa olevat luvut antavat saman
jakojäännöksen luvulla m jaettaessa. Kaikkien jäännösluokkien modulo m joukosta käytetään
merkintää  m. Jäännösluokan
m. Jäännösluokan 

 m edustajaksi voidaan valita mikä tahansa luku, joka on
kongruentti luvun a kanssa modulo m. Näistä luvuista voidaan jakoalgoritmin mukaan valita
yksikäsitteisesti luvun a pienin ei-negatiivinen jäännös modulo m. Tämä jäännös r toteuttaa
ehdon 0 < r < m. Siis jokaisella luokalla
m edustajaksi voidaan valita mikä tahansa luku, joka on
kongruentti luvun a kanssa modulo m. Näistä luvuista voidaan jakoalgoritmin mukaan valita
yksikäsitteisesti luvun a pienin ei-negatiivinen jäännös modulo m. Tämä jäännös r toteuttaa
ehdon 0 < r < m. Siis jokaisella luokalla 

 m on pienin ei-negatiivinen jäännös r modulo m,
joka toteutaa saman ehdon. Toisaalta nämä jäännökset ovat selvästi parittain epäkongruentteja
modulo m. Täten
m on pienin ei-negatiivinen jäännös r modulo m,
joka toteutaa saman ehdon. Toisaalta nämä jäännökset ovat selvästi parittain epäkongruentteja
modulo m. Täten

Esimerkki.  3 = {
3 = { ,
, ,
, }, missä
}, missä

Joukko  3 voidaan esittää myös esimerkiksi muodossa {
3 voidaan esittää myös esimerkiksi muodossa { ,
, ,
, } tai {
} tai { ,
, ,
,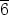 }.
}.
Jos m = 1, niin kongruenssi modulo m on triviaali: a  b (mod 1) kaikilla a,b
b (mod 1) kaikilla a,b 
 . Erityisesti
siis
. Erityisesti
siis  1 = {
1 = { }, missä
}, missä  =
=  .
.
Lause. Jäännösluokkien summa  +
+  =
=  ja tulo
ja tulo  .
.  =
=  eivät ole riippuvia
jäännösluokkien edustajien valinnasta. (Sanotaan, että jäännösluokkien summa ja tulo ovat
hyvin määriteltyjä.)
eivät ole riippuvia
jäännösluokkien edustajien valinnasta. (Sanotaan, että jäännösluokkien summa ja tulo ovat
hyvin määriteltyjä.)
Todistus. Olkoot  =
=  ja
ja  =
=  . Silloin a
. Silloin a  a' (mod m) ja b
a' (mod m) ja b  b' (mod m). Sivulla
Kongruenssi olevan lauseen kohdan (i) mukaan on
b' (mod m). Sivulla
Kongruenssi olevan lauseen kohdan (i) mukaan on

Täten  =
=  ja
ja 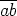 =
=  , mikä todistaa väitteen.
, mikä todistaa väitteen. ![[]](images/msam10-c-3.gif)
Linkit:
Konruenssi
Ekvivalenssiluokka
Jakoalgoritmi
Diofantoksen yhtälö