| Sanna Ranto, LUKUTEORIA JA ALGEBRA Versio 1, 1.11.2003 | LUKUTEORIA |
Diofantoksen yhtälö
Diofantoksen yhtälö on yhtälö, jolle etsitään kokonaislukuratkaisua. Lineaarisen kahden tuntemattoman Diofantoksen yhtälön ax + my = c (luvut a,m ja c ovat tunnettuja) ratkaiseminen on ekvivalenttia kongruenssin
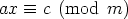
ratkaisemisen kanssa. Seuraavaksi todistetaan tätä kongruenssia koskeva tulos.
Lause. Jos syt(a,m) = 1, kongruensilla ax  c (mod m) on yksikäsitteinen ratkaisu x
c (mod m) on yksikäsitteinen ratkaisu x 
 välillä 0 < x < m - 1.
välillä 0 < x < m - 1.
Todistus. Oletuksen syt(a,m) = 1 nojalla on olemassa sellaiset luvut u ja v, että au + mv = 1.
Täten a(uc) + m(vc) = c ja kongruenssin ax  c (mod m) yksi ratkaisu on x = uc. Lisäksi
kongruenssin kaikki ratkaisut ovat keskenään kongruentteja. Nimittäin, jos x1 ja x2 ovat
kongruenssin kaksi eri ratkaisua, niin ax1
c (mod m) yksi ratkaisu on x = uc. Lisäksi
kongruenssin kaikki ratkaisut ovat keskenään kongruentteja. Nimittäin, jos x1 ja x2 ovat
kongruenssin kaksi eri ratkaisua, niin ax1  ax2 (mod m). Sivulla Kongruenssi olevan lauseen
kohdan (ii) mukaan tästä seuraa, että x1
ax2 (mod m). Sivulla Kongruenssi olevan lauseen
kohdan (ii) mukaan tästä seuraa, että x1  x2 (mod m). Ratkaisuista on siis tarkalleen yksi
halutulla välillä.
x2 (mod m). Ratkaisuista on siis tarkalleen yksi
halutulla välillä. ![[]](images/msam10-c-3.gif)
Linkit:
Suurin yhteinen tekijä
Kongruenssi
Esimerkki Diofantoksen yhtälön ja kongruenssin käytöstä