Aliryhmä

Määritelmä. Olkoon (G,*) ryhmä. Jos H G ja (H,*) on ryhmä sanotaan, että (H,*) on ryhmän (G,*) aliryhmä. Tätä merkitään (H,*) < (G,*). Jos lisäksi H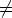G, voidaan merkitä (H,*) < (G,*).

Aliryhmän määrittelyssä pitää kiinnittää erityistä huomiota ryhmän binäärioperaatioon ja siihen, että aliryhmä määräytyy nimenomaan saman operaation suhteen. Esimerkiksi kokonaislukujen joukon osajoukko A = {-1, 1} muodostaa ryhmän kertolaskun suhteen, mutta se ei ole ryhmän (, +) aliryhmä, ja kuten esimerkeissä todettiin pari (, ^. ) ei ole ryhmä.

Ryhmän (G,*) ja sen aliryhmän (H,*) neutraalialkiot ovat sama alkio. Tämä nähdään seuraavasti. Oletetaan, että e on ryhmän (G,*) neutraalialkio ja e' on aliryhmän (H,*) neutraalialkio. Koska e' H G, voidaan ryhmässä G laskea, että e' = e'* e'. Kertomalla yhtälö puolittain alkion e' käänteisalkiolla (e')^-1 saadaan e = (e')^-1 * e' = (e')^-1 * (e'* e') = ((e')^-1 * e') * e' = e * e' = e'.

Edellisestä seuraa, että joukon H alkion a käänteisalkio on sama aliryhmässä (H,*) ja ryhmässä (G,*).

Ryhmän (G,*) triviaalit aliryhmät ovat ryhmä itse ja sen neutraalialkion muodostama ryhmä.

Seuraavaa lausetta käyttäen voidaan usein selvittää muodostaako annettu joukko aliryhmän.

Lause. [Aliryhmäkriteeri] Olkoon (G,*) ryhmä ja H G. Pari (H,*) on ryhmän (G,*) aliryhmä jos ja vain jos H on epätyhjä joukko ja a * b^-1 H kaikilla a,b H.

Todistus. Oletetaan ensin, että (H,*) on ryhmän (G,*) aliryhmä. Koska (H,*) on ryhmä, on siinä neutraalialkio, siis H on epätyhjä joukko. Jos b H, niin b^-1 H, koska (H,*) on ryhmä. Jos edelleen a H, niin koska H on ryhmänä suljettu operaation * suhteen, a * b^-1 H.

Todistetaan väite vielä toiseen suuntaan. Oletetaan, että H on epätyhjä joukko ja a * b^-1 H kaikilla a,b H. Olkoon e ryhmän (G,*) neutraalialkio. Jos a H, niin oletuksen nojalla e = a * a^-1 H, joten joukossa H on neutraalialkio. Edelleen oletuksen nojalla a^-1 = e * a^-1 H, joten kaikilla joukon H alkioilla on käänteisalkio joukossa H. Nyt on näytetty ryhmän ehtojen (G2) ja (G3) toteutuvuus. Operaation * assosiatiivisuus joukossa H seuraa siitä, että joukon H alkiot ovat myös joukon G alkioita ja ovat näin assosiatiivisia ryhmän (G, *) binäärioperaation suhteen. Lopuksi todistetaan vielä, että H on suljettu operaation * suhteen. Jos a,b H, niin edellä todistetun nojalla b^-1 H. Oletuksen nojalla saadaan a * b = a * (b^-1)^-1 H. Täten (H,*) on ryhmä ja siis (H,*) < (G,*).

Linkit:
Ryhmä
Esimerkkejä aliryhmistä