| Sanna Ranto, LUKUTEORIA JA ALGEBRA Versio 1, 1.11.2003 | RYHMÄ |
Ryhmien homomorfialauseen seuraus
Jos (N,*)  (G,*), kuvausta
(G,*), kuvausta

missä (a * N) . (b * N) = a * b * N, sanotaan (luonnolliseksi) projektioksi ryhmältä (G,*)
tekijäryhmälle (G/N, . ). Kuvaus on triviaalisti surjektiivinen ja se on homomorfismi, sillä
kaikilla a,b  G :
G :

Kuvaus on siis epimorfismi.
Olkoon f : (G,*)  (G',•) ryhmähomomorfismi. Valitaan nyt N = ker(f). Silloin
homomorfialauseen nojalla
(G',•) ryhmähomomorfismi. Valitaan nyt N = ker(f). Silloin
homomorfialauseen nojalla

missä F on kuvaus (G/N, . )  (Im (f),•). Siis f = Fo
(Im (f),•). Siis f = Fo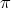 . Sama asia voidaan ilmaista
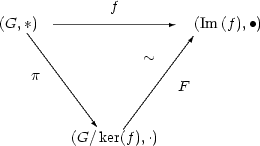
sanomalla, että oheinen diagramma kommutoi (alkioiden kuvautuminen ei riipu kuljetusta
reitistä).
. Sama asia voidaan ilmaista
sanomalla, että oheinen diagramma kommutoi (alkioiden kuvautuminen ei riipu kuljetusta
reitistä).
Homomorfialauseen nojalla ryhmän (G,*) jokainen homomorfinen kuva on isomorfinen jonkin
ryhmän (G,*) tekijäryhmän kanssa. Kääntäen, ryhmän (G,*) jokainen tekijäryhmä (G/N, . )
on isomorfinen ryhmän (G,*) jonkin homomorfisen kuvan kanssa. Nimittäin edellä esitetyn
nojalla G/N = Im (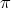 ), missä
), missä 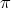 on projektio (G,*)
on projektio (G,*)  (G/N, . ).
(G/N, . ).
Linkit:
Ryhmien homomorfialause