Sanna Ranto, LUKUTEORIA JA ALGEBRA
Versio 1, 1.11.2003 		RYHMÄ
 

Ryhmien homomorfialause

Seuraavan lauseen mukaan jokainen homomorfismi antaa tietyn isomorfian. Lauseeseen sisältyy myös kuvauksen indusoinnin käsite. Tämä lause on ryhmäteorian peruslauseita.

Lause. [Ryhmien homomorfialause] Jos f : (G,*) --> (G,•) on ryhmähomomorfismi, niin

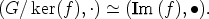
(G/ ker(f ),.) -~ (Im (f),•).

Tarkemmin: homomorfismi f indusoi isomorfismin

F: (G/ ker(f),.) --> (Im (f),•), F (a *ker(f)) = f (a) A a (- G.

Huomaa, että sivun Huomioita normaaleista aliryhmistä ja homomorfimista toisen lauseen mukaan (ker(f),*) on ryhmän (G,*) normaaali aliryhmä. Täten lauseen tekijäryhmän (G/ ker(f), . ) muodostaminen on mahdollista. Tässä operaatio  .  määritellään kuten sivun Tekijäryhmä lauseessa eli (a* ker(f)) . (b* ker(f)) = (a*b) * ker(f) kaikilla a,b (- G. Siirrytään sitten todistamaan itse lausetta.

Todistus. Todistetaan ensin, että kuvaus F on hyvin määritelty. Jos joillekin a,b (- G on a* ker(f) = b* ker(f) niin a (- b* ker(f) eli a = b*k, jollekin ytimen alkiolle k. Täten, jos e' on ryhmän (G',•) neutraalialkio,

' F(a*ker(f)) = f (a) = f (b * k) = f(b) • f(k) = f (b) • e = f (b) = F (b * ker(f)),

mikä todistaa hyvinmääriteltävyyden.

Osoitetaan seuraavaksi, että F on homomorfismi. Kaikilla a * ker(f),b * ker(f) (- G/ ker(f) saadaan

F((a*ker(f)).(b*ker(f ))) = F (a*b*ker(f )) = f (a*b) = f(a)•f(b) = F (a*ker(f))•F (b*ker(f)).

Täten F on homomorfismi.

Bijektiivisyyden osoittamiseksi näytetään, että F on injektio ja surjektio. Surjektiivisuus seuraa suoraan kuvauksen F määritelmästä. Injektiivisyys todetaan käyttämällä sivun Homomorfismin ydin ja kuva toista lausetta. Olkoon e' ryhmän (Im (f),•) neutraalialkio. Jos jollekin a (- G on F (a * ker (f)) = e' niin silloin f(a) = e'. Siis a (- ker(f), joten a * ker(f) = ker(f) on ryhmän (G/ ker (f),  .  ) neutraalialkio. Täten ker(F) = {ker(f)} ja saadaan injektiivisyys. []

Linkit:
Huomioita normaaleista aliryhmistä ja homomorfismista
Ryhmähomomorfismin ydin ja kuva
Tekijäryhmä
Ryhmien homomorfialauseen seuraus
Suunnikassääntö
Esimerkkejä ryhmien homomorfialauseen käytöstä