Huomioita normaaleista aliryhmistä ja homomorfismista

Lause. Olkoon f : (G,*) (G',•) ryhmähomomorfismi. Jos (N,*) (G,*), niin (f(N),•) (f(G),•).

Todistus. Ryhmien homomorfia -sivun lauseen perusteella on (f(N),•) < (f(G),•). Vielä pitää todistaa, että kaikilla b f(G) ja y f(N) on b•y •b^-1 f(N). On olemassa sellaiset a G ja x N, että b = f(a) ja y = f(x). Silloin

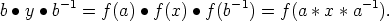
Koska aliryhmä (N,*) on normaali, niin a * x * a^-1 N. Täten f(a * x * a^-1) f(N).

Lause. Olkoon f : (G,*) (G',•) ryhmähomorfismi. Silloin (ker(f),*) (G,*).

Todistus. Sivun Homomorfismin ydin ja kuva ensimmäisen lauseen perusteella (ker(f),*) on ryhmän (G,*) aliryhmä.

Olkoon e' ryhmän (G',•) neutraalialkio ja oletetaan, että a G ja x ker(f). Nyt

joten a * x * a^-1 ker(f) ja normaalisuuskriteerin nojalla (ker(f),*) on normaali.

Linkit:
Aliryhmä
Ryhmien homomorfia
Homomorfismin ydin ja kuva
Normaali aliryhmä