| Sanna Ranto, LUKUTEORIA JA ALGEBRA Versio 1, 1.11.2003 | RYHMÄ |
Ryhmien homomorfia
Määritelmä. Olkoot (G,*) ja (G',•) ryhmiä. Kuvausta f : (G,*)  (G',•) sanotaan
(ryhmä)homomorfismiksi, jos se toteuttaa ehdon
(G',•) sanotaan
(ryhmä)homomorfismiksi, jos se toteuttaa ehdon
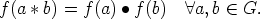
Olkoon e ryhmän (G,*) neutraalialkio ja e' ryhmän (G,•) neutraalialkio. Ryhmähomomorfismi
kuvaa neutraalialkion neutraalialkioksi ja käänteisalkiot käänteisalkioiksi. Siis, jos f on
homomorfismi ja a  G, niin
G, niin

Ensimmäinen yhtälöistä nähdään oikeaksi operoimalla yhtälöä f(e) • f(e) = f(e * e) molemmin puolin käänteisalkiolla f(e)-1. Jälkimmäinen seuraa puolestaan siitä, että f(a) • f(a-1) = f(a * a-1) = f(e) = e' ja samoin f(a-1) • f(a) = e'.
Lause. Olkoon f : (G,*)  (G',•) homomorfismi. Jos (H,*) < (G,*), niin (f(H),•) < (G',•).
(G',•) homomorfismi. Jos (H,*) < (G,*), niin (f(H),•) < (G',•).
Todistus. Koska (H,*) on ryhmä, niin H on epätyhjä joukko. Täten myös f(H) on
epätyhjä. Olkoon a',b' f(H). Silloin joillekin a,b
f(H). Silloin joillekin a,b  H on a' = f(a) ja b' = f(b).
Nyt
H on a' = f(a) ja b' = f(b).
Nyt

joten väite seuraa aliryhmäkriteeristä. ![[]](images/msam10-c-3.gif)
Linkit:
Aliryhmä
Homomorfismin ydin ja kuva
Huomioita ryhmähomomorfismista
Esimerkkejä ryhmähomomorfismeista