Sanna Ranto, LUKUTEORIA JA ALGEBRA
Versio 1, 1.11.2003 		RYHMÄ
 

Ryhmähomomorfismin ydin ja kuva

Määritelmä. Olkoon f : (G,*) --> (G',•) homomorfismi ja e' ryhmän (G',•) neutraalialkio. Silloin kuvauksen ydin (kernel), ker(f), on joukko

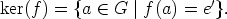
ker(f) = {a (- G |f(a) = e'}.

Kuvauksen f kuva (image), Im (f), on joukko

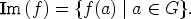
Im (f ) = {f(a) |a (- G}.

Ryhmien homomorfia -sivun lauseen perusteella on (Im (f),•) = (f(G),•) ryhmän (G',•) aliryhmä.

Lause. Olkoon f : (G,*) --> (G',•) ryhmähomomorfismi. Silloin (ker(f),*) on ryhmän (G,*) aliryhmä.

Todistus. Sivun Ryhmien homomorfia huomion nojalla ryhmän (G,*) neutraalialkio e kuvautuu homomorfismissa f ryhmän (G',•) neutraalialkioksi e'. Siis e (- ker(f), joten joukko ker(f) on epätyhjä.

Oletetaan, että a,b (- ker(f). Homomorfismin ja ytimen määritelmien sekä sen tiedon, että homomorfia kuvaa käänteisalkion käänteisalkioksi, perusteella saadaan:

f (a * b-1) = f(a) • f (b- 1) = f(a) • f(b)-1 = e'• (e')-1 = e'.

Täten a * b-1 (- ker(f) ja väite seuraa aliryhmäkriteeristä. []

Lause. Ryhmähomomorfismi f : (G,*) --> (G',•) on injektio jos ja vain jos ker(f) = {e}, missä e on ryhmän (G,*) neutraalialkio.

Todistus. Olkoon e' ryhmän (G',•) neutraalialkio.

Oletetaan ensin, että f on injektio. Koska homomorfismi säilyttää neutraalialkion, niin f(e) = e'. Jos toisaalta on olemassa jokin joukon G alkio x, jolle f(x) = e', niin injektiivisyydestä seuraa, että x = e. Siis ker(f) = {e}.

Oletetaan kääntäen, että ker(f) = {e}. Olkoot x1,x2 (- G. Ehdosta f(x1) = f(x2) seuraa, että f(x1 ) • f(x2 )-1 = e'. Koska homomorfismi kuvaa käänteisalkion käänteisalkioksi, saadaan f(x1 ) • f(x-1 2) = e'. Homomorfian perusteella on f(x1 * x-1 2) = e'. Oletuksesta ker(f) = {e} seuraa nyt, että x1 * x-1 2 = e, joten x1 = x2. Siis f on injektio. []

Linkit:
Ryhmien homomorfia
Aliryhmä