smr217.html

Sanna Ranto, LUKUTEORIA JA ALGEBRA
Versio 1, 1.11.2003

RYHMÄ

Esimerkkejä ryhmähomomorfismeista

Esimerkki. Positiiviset reaaliluvut muodostavat kertolaskun suhteen ryhmän (₊,^.). Samoin kaikki reaaliluvut muodostavat yhteenlaskun suhteen ryhmän (, +). Olkoon f kuvaus ryhmältä (₊,^.) ryhmälle (, +), missä f(x) = log x kaikilla x ₊. Logaritmin määritelmän perusteella f(xy) = log(xy) = log x + log y = f(x) + f(y). Täten kuvaus f on homomorfismi. Tarkastamalla bijektiivisyys huomataan, että kuvaus on isomorfismi.

Esimerkki. Olkoon f : (, +) --> (_m, +), missä ryhmän (_m, +) yhteenlasku on jäännösluokkien yhteenlasku ja missä f(a) = --
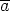a kaikilla a . Kuvaus f on homomorfismi, koska kaikilla x,y on f(x + y) = x-+-y- = + = f(x) + f(y).

Esimerkki. Näytetään, etteivät ryhmät (, +) ja (^*,^.), missä ^* = \{0}, ole isomorfisia. Pitää siis osoittaa, ettei ole olemassa mitään isomorfista kuvausta toiselta ryhmältä toiselle.

Ryhmän (^*,^.) neutraalialkio on 1. Tässä ryhmässä on kaksi alkiota x = 1 ja x = -1, jotka toteuttavat yhtälön x² = 1. Jos olisi jokin isomorfismi f ryhmältä (^*,^.) ryhmälle (, +) niin f(1) = f(1^.1) = f(-1^.(-1)) = f(1) + f(1) = f(-1) + f(-1). Toisaalta ryhmän (, +) neutraalialkio on 0 ja homomorfismi kuvaa neutraalialkion neutraalialkioksi, joten f(1) = 0. Jotta f voisi olla isomorfismi pitäisi ryhmässä (, +) olla kaksi eri ratkaisua yhtälölle x + x = 0, ratkaisuja on kuitenkin vain yksi x = 0. Täten (, +) / (^*,^.).

Esimerkki. Olkoon (G,*) ryhmä ja u G. Osoitetaan, että kuvaus

-1 fu : (G, *) --> (G, *), fu(a) = u * a *u A a (- G,

on isomorfismi.

Osoitetaan ensin, että kuvaus f_u on homomorfismi. Tämä tehdään suoraan laskemalla. Kaikilla a,b G :

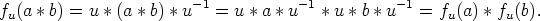
fu(a* b) = u *(a * b) * u-1 = u * a * u-1 *u * b * u- 1 = fu(a) * fu(b).

Kuvauksen bijektiivisyyden toteamiseksi osoitetaan, että kuvauksella f_u on käänteiskuvaus. Näytetään, että kuvauksen f_u käänteiskuvaus on f -1
u , jolle f -1
u (a) = u^-1 * a * u kaikille a G :

(fuof-u 1)(a) = fu(fu-1(a)) = fu(u-1 *a * u) = u * u- 1 * a * u *u -1 = a

ja samoin voidaan osoittaa, että (f -1
u of_u)(a) = a. Koska molemmat yhdistetyt kuvaukset f_u o f -1
u ja f -1
u of_u tuottavat identiteettikuvauksen on f -1
u kuvauksen f_u käänteiskuvaus. Täten f_u on bijektio.

Isomorfista kuvausta ryhmältä itselleen sanotaan automorfismiksi. Esimerkin kuvaus on siis automorfismi.

Linkit:
Ryhmien homomorfia
Huomioita ryhmähomomorfismista