smr224.html

Sanna Ranto, LUKUTEORIA JA ALGEBRA
Versio 1, 1.11.2003

RYHMÄ

Suunnikassääntö

Soveltamalla homomorfialausetta erilaisiin homomorfismeihin saadaan erilaisia isomorfialakeja. Esitetään näistä seuraavaksi yksi.

Olkoon (H,*) < (G,*) ja (K,*) <|_ (G,*). Silloin joukko

H * K = {h *k | h (- H, k (- K}

muodostaa ryhmän (G,*) aliryhmän operaation * suhteen. Tämä voidaan todeta aliryhmäkriteerin avulla. Oletetaan, että h₁ * k₁,h₂ * k₂ H * K. Nyt

(h*k)*(h * k )-1 = h * k * k-1 *h -1 koska (h * k )-1 = k- 1* h-1 112 2 1 1 2-1 2 -1 -1 2 2 2 2 = h1 * k1 * h2-1 *h2 * k2 *h 2 -1 -1 = h1 * k1 * h2 *k3 missä k3 = h2 *k2 * h2 (- K = h1 * h-21 *h2 * k1 * h-21 *k3 = h1 * h-1 *k4 *k3 missä k4 = h2 *k1 *h -1 (- K. 2 2

Koska (H,*) on aliryhmä, h₁ * h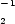 -1
2 H, ja koska k₄ * k₃ K, saadaan väite eli (h₁ * k₁) * (h₂ * k₂)^-1 H * K.

Oletuksesta (K,*) <|_ (G,*) ja siitä, että K H * K G seuraa, että (K,*) on myös ryhmän (H * K,*) normaali aliryhmä. Määritellään tekijäryhmän ((H * K)/K,^.) operaatio ^. kuten sivun Tekijäryhmä lauseessa. Kuvaus

f : (H, *) --> ((H *K)/K, .), f (a) = a * K A a (- H,

on homomorfismi. Kuvauksen ydin ja kuva ovat ker(f) = H $/~\$ K ja Im (f) = (H * K)/K (todista nämä itsellesi). Täten homomorfialauseen mukaan

(H/(H /~\ K), .) - ~ ((H * K)/K, .).

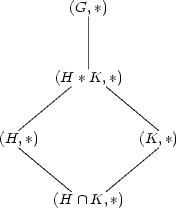
Oheisesta diagrammasta selviää, miksi sääntöä sanotaan suunnikassäännöksi.

Linkit:
Ryhmien homomorfialause
Tekijäryhmä