| Sanna Ranto, LUKUTEORIA JA ALGEBRA Versio 1, 1.11.2003 | RENGAS |
Renkaan yksikköryhmä
Yhden alkion joukko R = {a} muodostaa triviaalisti renkaan, kun määritellään a + a = a ja a . a = a. Koska a on silloin ryhmän (R, +) neutraalialkio eli nolla-alkio, sanotaan tätä rengasta nollarenkaaksi.
Oletetaan jatkossa, ettei R ole nollarengas.
Määritelmä. Renkaan (R, +, . ) alkiota u sanotaan renkaan yksiköksi (unit), jos alkiolla u on
käänteisalkio renkaassa R, toisin sanoen, jos on olemassa sellainen u-1  R, että
u . u-1 = u-1 . u = 1
R.
R, että
u . u-1 = u-1 . u = 1
R.
Renkaan kaikkien yksiköiden joukosta käytetään merkintää R*.
Lause. Olkoon (R, +, . ) rengas. Silloin (R*, . ) on ryhmä. Tätä ryhmää sanotaan renkaan yksikköryhmäksi.
Todistus. Joukko R* on epätyhjä, sillä 1
R  R*. Alkio 1
R on ryhmän (R*, . ) neutraalialkio.
Jos u,v
R*. Alkio 1
R on ryhmän (R*, . ) neutraalialkio.
Jos u,v  R*, niin u . v
R*, niin u . v  R*, sillä alkion u . v käänteisalkio on v-1u-1.
R*, sillä alkion u . v käänteisalkio on v-1u-1.
Operaatio . on assosiatiivinen joukossa R, joten se on assosiatiivinen myös osajoukossa R*.
Jos u  R*, niin u-1
R*, niin u-1  R, koska alkion u-1 käänteisalkio (u-1)-1 = u
R, koska alkion u-1 käänteisalkio (u-1)-1 = u 
 .
.
Täten (R*, . ) toteuttaa ryhmän postulaatit ja on siis ryhmä. ![[]](images/msam10-c-3.gif)
Lause. Olkoon (R, +, . ) rengas (R ei ole nollarengas). Silloin renkaan ykkösalkio 1 R ja nolla-alkio 0R ovat aina eri alkiot.
Todistus. Jos olisi 1R = 0R, niin kaikilla renkaan R nollasta eroavilla alkioilla a olisi
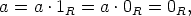
mikä on ristiriita. ![[]](images/msam10-c-3.gif)