Ihanteen generointi ja pääihannerengas

Ryhmäteoriassa todettiin, että joukon G osajoukko generoi ryhmän (G,*) aliryhmän. Ihanteille saadaan vastaava tulos. Olkoon (R, +, ^. ) rengas ja S R. Silloin S generoi renkaan R ihanteen < S >, missä

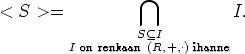
Sivun Ihanne viimeisen lauseen mukaan < S > on ihanne. Tämä ihanne on renkaan (R, +, ^. ) suppein sellainen ihanne, joka sisältää joukon S.

Jos S on äärellinen joukko S = {a₁,a₂,...,a_n}, niin ihanteen < S > sanotaan olevan äärellisesti generoitu(va). Tällöin voidaan merkitä < S >=< a₁,...,a_n > .

Yhden alkion a generoimaa ihannetta < a > sanotaan pääihanteeksi.

Huomaa, että

jos kumpikin ihanne sisältää toisen generaattorit. Nimittäin, jos a₁,...,a_n < b₁,...,b_m >, niin edellä todetun nojalla < a₁,...,a_n >< b₁,...,b_m > . Vastaava tulos saadaan toisin päin.

Triviaalit ihanteet R ja {0_R} ovat pääihanteita, koska R =< 1_R > ja {0_R} =< 0_R > .

Määritelmä. Rengasta, jonka kaikki ihanteet ovat pääihanteita, sanotaan pääihannerenkaaksi (principal ideal ring).

Lause. Jos (R, +, ^. ) on kommutatiivinen rengas ja {a ₁,...,a_k} R on epätyhjä joukko, niin

Todistus. Merkitään U = {r₁a₁ + + r_ka_k | r_i R, i = 1,...,k}. Selvästi U on epätyhjä joukko. Olkoot r₁a₁ + 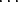+ r_ka_k U ja s₁a₁ + + s_ka_k U. Renkaan R distributiivilaeista seuraa, että

sillä r_i - s_i R kaikilla luvun i arvoilla.

Olkoon r R. Renkaan R distributiivi- ja assosiatiivilaeista seuraa, että

sillä rr_i R kaikilla arvoilla i. Ihannekriteerin nojalla U on ihanne.

Kaikilla luvun i arvoilla 0_Ra₁ + + 0_Ra_i-1 + 1_Ra_i + 0_Ra_i+1 + + 0_ra_k U, missä 0_R on renkaan R nolla-alkio ja 1_R on ykkösalkio. Täten {a₁,...,a_k} U. Koska U on ihanne, < a₁ , ... , a_k > U.

Toisaalta jokainen joukko I, joka sisältyy leikkaukseen

sisältää kaikki joukon U alkiot. Täten U < a₁,...,a_k > ja siis < a₁,...,a_k >= U.

Linkit:
Ryhmän generointi
Ihanne