| Sanna Ranto, LUKUTEORIA JA ALGEBRA Versio 1, 1.11.2003 | RENGAS |
Ihanne
Ryhmäteoriassa normaaleilla aliryhmillä on erityisasema. Rengasteoriassa normaaleja aliryhmiä vastaavat ihanteet.
Määritelmä. Olkoon (R, +, . ) rengas. Joukkoa I  R sanotaan renkaan R ihanteeksi tai
ideaaliksi, jos
R sanotaan renkaan R ihanteeksi tai
ideaaliksi, jos
(I1) (I, +) on ryhmän (R, +) aliryhmä ja
(I2) ra  I ja ar
I ja ar  I kaikilla r
I kaikilla r  R ja a
R ja a  I.
I.
(Jos ehdosta (I2) jätetään pois ehto ar  I, saadaan yleisempi vasemman ihanteen
käsite. Vastaavasti oikea ihanne saadaan jättämällä ehdosta (I2) pois ehto ra
I, saadaan yleisempi vasemman ihanteen
käsite. Vastaavasti oikea ihanne saadaan jättämällä ehdosta (I2) pois ehto ra  I.)
I.)
Jokaisen renkaan (R, +, . ) triviaalit ihanteet ovat rengas itse ja nollaihanne {0 R}.
Jos renkaan (R, +, . ) ihanne I muodostaa alirenkaan operaatioiden + ja . suhteen, niin
alirengaskriteerin nojalla 1R  I. Tästä seuraa ehdon (I2) nojalla, että r = r . 1
R
I. Tästä seuraa ehdon (I2) nojalla, että r = r . 1
R  I kaikilla
r
I kaikilla
r  R. Täten rengas itse on sen ainoa ihanne, joka on myös (ali)rengas.
R. Täten rengas itse on sen ainoa ihanne, joka on myös (ali)rengas.
Edellisen päättelyn nojalla saadaan seuraava tulos: Jos I on renkaan R aito ihanne (siis
I  R), niin I
R), niin I R* = Ø (R* on renkaan yksiköiden joukko). Nimittäin, jos renkaan yksikkö
u
R* = Ø (R* on renkaan yksiköiden joukko). Nimittäin, jos renkaan yksikkö
u  I, niin ehdon (I2) nojalla u . u-1 = 1
R
I, niin ehdon (I2) nojalla u . u-1 = 1
R  I, ja silloin olisi I = R.
I, ja silloin olisi I = R.
Lause. (Ihannekriteeri) Olkoon (R, +, . ) rengas ja I  R. Joukko I on renkaan R ihanne jos
ja vain jos seuraavat ehdot toteutuvat:
R. Joukko I on renkaan R ihanne jos
ja vain jos seuraavat ehdot toteutuvat:
(a) I on epätyhjä joukko,
(b) a - b  I kaikilla a,b
I kaikilla a,b  I ja
I ja
(c) ra  I ja ar
I ja ar  I kaikilla r
I kaikilla r  R ja a
R ja a  I.
I.
Todistus. Ehdot (a) ja (b) ovat yhdessä ekvivalentit ehdon (I1) kanssa. Ehto (c) on sama kuin
ehto (I2). ![[]](images/msam10-c-3.gif)
Lause. Jos joukot I ja J ovat renkaan (R, +, . ) ihanteita, niin samoin on niiden leikkaus
I  J ja summa
J ja summa
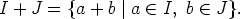
Sama on voimassa useammankin kuin kahden ihanteen tapauksessa (leikkauksen suhteen jopa äärettömän monen ihanteen leikkaus on ihanne).
Todistus. Todistetaan summaa koskeva väite. Leikkausta koskeva väite voidaan todistaa samantapaisella päättelyllä. Koska I ja J ovat ihanteina epätyhjiä joukkoja, on niiden summakin epätyhjä.
Olkoot a1 , a2  I, b1,b2
I, b1,b2  J ja ci = ai + bi
J ja ci = ai + bi  I + J (i = 1, 2). Käyttäen hyväksi sivulla Renkaan
aritmetiikkaa esiteltyjä laskulakeja ja ryhmän (R, +) kommutatiivisuutta saadaan:
c1 - c2 = a1 + b1 - (a2 + b2) = a1 + b1 - a2 - b2 = a1 - a2 + b1 - b2
I + J (i = 1, 2). Käyttäen hyväksi sivulla Renkaan
aritmetiikkaa esiteltyjä laskulakeja ja ryhmän (R, +) kommutatiivisuutta saadaan:
c1 - c2 = a1 + b1 - (a2 + b2) = a1 + b1 - a2 - b2 = a1 - a2 + b1 - b2  I + J. Kaikilla
r
I + J. Kaikilla
r  R on rc1 = r(a1 + b1) = ra1 + rb1
R on rc1 = r(a1 + b1) = ra1 + rb1  I + J. Väite seuraa ihannekriteeristä.
I + J. Väite seuraa ihannekriteeristä. ![[]](images/msam10-c-3.gif)
Linkit:
Aliryhmä
Normaali aliryhmä
Alirengas
Renkaan aritmetiikkaa
Rengas