| Sanna Ranto, LUKUTEORIA JA ALGEBRA Versio 1, 1.11.2003 | RENGAS |
Renkaan aritmetiikkaa
Olkoon (R, +, . ) rengas. Koska (R, +) on ryhmä noudattaa yhteenlasku ryhmäteoriasta
tuttuja sääntöjä. Esimerkiksi alkioiden a,b  R erotus määritellään kuten ryhmässä:
a - b = a + (-b).
R erotus määritellään kuten ryhmässä:
a - b = a + (-b).
Myös kertolaskun säännöt perustuvat ryhmäteoriaan. Huomaa, että alkion a  R negatiivinen
potenssi on määritelty vain jos alkiolla a on käänteisalkio a-1.
R negatiivinen
potenssi on määritelty vain jos alkiolla a on käänteisalkio a-1.
Soveltamalla renkaan distributiivilakia (R5) toistuvasti saadaan kaavat kaikille
a,a1,...,am,b,b1,...,bn  R:
R:

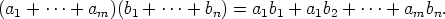
Seuraavassa lauseessa saadaan lisää tarvittavia laskulakeja renkaaseen.
Lause. Olkoot (R, +, . ) rengas, 0
R sen nolla-alkio ja a,b,c  R. Silloin
R. Silloin
(i) 0R . a = a . 0
R = 0R,
(ii) a(-b) = (-a)b = -(ab) ja (-a)(-b) = ab,
(iii) a(b - c) = ab - ac ja (a - b)c = ac - bc.
Todistus. (i) Koska 0R = 0R + 0R, niin käyttämällä distributiivilakia saadaan: 0R . a = (0 R + 0R) . a = 0 R . a + 0 R . a. Vähentämällä saadun yhtälön molemmilta puolilta 0R . a päädytään yhtälöön 0 R = 0R . a. Väite a . 0 R = 0R voidaan todistaa samoin.
(ii) Koska distributiivilain ja edellisen kohdan nojalla on ab + a(-b) = a(b + (-b)) = a . 0 R = 0R, niin tulo a(-b) on tulon ab vasta-alkio Abelin ryhmässä (R, +). Vastaavasti nähdään, että myös (-a)b on tulon ab vasta-alkio.
Edellisten yhtälöiden avulla saadaan (-a)(-b) = -(a(-b)) = -(-(ab)) = ab.
(iii) Nyt a(b - c) = a(b + (-c)) = ab + a(-c) = ab + (-(ac)) = ab - ac. Toinen yhtälö voidaan
todistaa samoin. ![[]](images/msam10-c-3.gif)
Renkaan (R, +, . ) alkiot toteuttavat ryhmäteoriasta tutut laskulait:
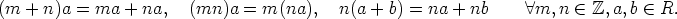
Lisäksi kaikilla a,b  R ja m,n
R ja m,n 
 on voimassa
on voimassa

 + a. Ykkösalkiota käyttäen voidaan tulo na esittää renkaan
operaationa, nimittäin na = (n1R) . a = (1
R +
+ a. Ykkösalkiota käyttäen voidaan tulo na esittää renkaan
operaationa, nimittäin na = (n1R) . a = (1
R +  + 1R) . a. Negatiivisilla n :n arvoilla tulo na
on alkion |n|a vasta-alkio.
+ 1R) . a. Negatiivisilla n :n arvoilla tulo na
on alkion |n|a vasta-alkio.
Linkit:
Rengas
Renkaan yksikköryhmä