Rekan puoliperävaunu
Insinööriosastojen valintakoetehtävä vuodelta 1997
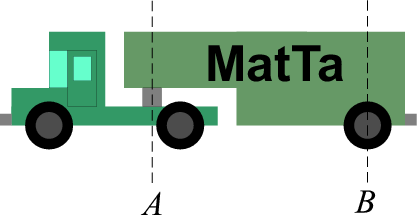
Rekan puoliperävaunu on kiinnitetty vetoautoon tapilla A, joka alkuhetkellä
on xy -tason origossa. Perävaunun taka-akselin keskipiste B on alkuhetkellä x
-akselin pisteessä (a, 0), missä a > 0. Kun vetovaunu lähtee liikkeelle, A liikkuu y
-akselia pitkin ylöspäin, ja B liikkuu siten, että joka hetki sen liikesuunta on
kohti A:n senhetkistä sijaintia. Osoita, että B kulkee pitkin käyrää y = f(x),
missä
f(x) = aln 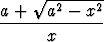 -
- 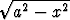 .
.
Ratkaisu
Olkoon y = g(x) käyrä, jota pitkin piste B liikkuu; on näytettävä
g(x) = f(x).
Funktio g toteuttaa ehdon
g'(x) = -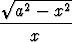
Lisäksi on selvää, että g(a) = 0.
Toisaalta, derivoimalla annettu f:n lauseke nähdään, että
f'(x) = -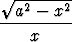 ;
;
Lisäksi sijoittamalla x = a saadaan f(a) = 0.
Koska g'(x) = f'(x), on g(x) = f(x) + C, missä C on vakio. Koska lisäksi g(a) = f(a), on
oltava C = 0. Siis g(x) = f(x). 

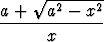 -
- 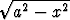 .
.
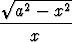
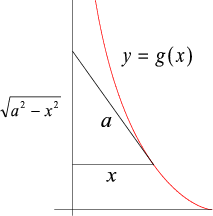
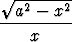 ;
;
