Vakiokertoiminen lineaariyhtälö ja faasitasoesitys

Vakiokertoimisen homogeeniyhtälön y'' + 2y' + y = 0 karakteristinen yhtälö on r² + 2r + 1 = 0. Tällä on kaksinkertainen juuri r = -1, jolloin yleinen ratkaisu on

y = C₁e^-t + C₂te^-t,

missä riippumatonta muuttujaa on merkitty t:llä. Ratkaisun derivaatta on

z = y' = (C₂ - C₁)e^-t - C₂te^-t.

Yhtälöä vastaava normaaliryhmä on

Tämä on autonominen ja antaa siis mahdollisuuden piirtää faasitasoon ratkaisujen suuntakenttä. Faasitasossa olevat ratkaisukäyrät ovat käyriä, joiden parametriesitys saadaan yhtälön ratkaisusta:

Tässä t on käyräparametrin asemassa. Alkuehto y(0) = y₀, z(0) = z₀ määrää suuntakenttäkuviossa pisteen (y₀, z₀), jonka kautta ratkaisukäyrä kulkee, ja toisaalta vakioiden C₁ ja C₂ arvot parametriesityksessä.

Faasitasoesitys näyttää seuraavalta:

Kaikki ratkaisukäyrät suuntautuvat origoon, koska lim_t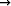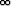y(t) = lim_t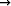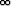z(t) = 0. Lukija pohtikoon, milloin origon lähestyminen on suoraviivaista ja miten tämä ilmenee funktioiden y(t) ja z(t) lausekkeista.

Faasitason ratkaisukäyrien yhtälö F (y, z) = 0 voidaan löytää ratkaisemalla normaaliryhmä. Tämä voidaan nimittäin palauttaa yhteen ensimmäisen kertaluvun yhtälöön puolittain jakamalla:

= -.

Tulokseksi saadaan

+ ln|y + z| + C = 0.