Tavallinen heiluri

Otetaan tarkastelun kohteeksi tavallinen yksinkertainen heiluri. Tämä koostuu kitkattomaan niveleen kiinnitetystä (massattomasta) varresta sekä sen päässä olevasta kuulasta. Olkoon varren pituus L ja sen päässä olevan kuulan massa m. Kun heiluri poikkeutetaan tasapainoasemastaan ja se vapautetaan, syntyy heiluriliike. Rajoitutaan tarkastelemaan tasossa tapahtuvaa liikettä, jolloin heilurin asema voidaan ilmaista kulmalla , joka osoittaa poikkeaman pystysuorasta suunnasta.

Heilurin kuulaan vaikuttaa painovoima mg. Tämä voima yhdessä varren tukivoiman kanssa aiheuttaa tangentiaalisen voiman heilurin ympyräkaaren muotoiselle liikeradalle. Newtonin toisen lain mukaisesti tämän voiman tasapainottaa heilurin kulmakiihtyvyys , jota vastaava voima on . Nämä voimat siis kumoavat toisensa, jolloin saadaan differentiaaliyhtälö

eli

Tämän differentiaaliyhtälön ratkaisu ei ole alkeisfunktio. Jos kulma on pieni, yhtälössä käytetään usein approksimaatiota , jolloin alkeisfunktiot tarjoavat approksimatiivisen ratkaisun

Lasketaan tarkalle heiluriyhtälölle numeerinen ratkaisu ja tarkastellaan kulman aikariippuvuutta. Tämän jälkeen rakennetaan tarkkaan ratkaisuun perustuen animaatio heilurin liikkeelle.

Laskujen aluksi on syytä hävittää mahdollisista aiemmista laskuista jääneet muuttujat.

Heiluria kuvaava toisen kertaluvun differentiaaliyhtälö on helposti ilmaistavissa normaaliryhmänä.

Ongelman tuntemattomat funktiot ovat heilurin kulma ja kulmanopeus.

Olkoon . Alkuehdon määrittää tilanne, jossa heiluri on levossa poikkeutettuna yhden radiaanin kulmaan.

Ratkaistaan differentiaaliyhtälö numeerisesti.

Muokataan ratkaisu käyttökelpoisempaan muotoon.

Piirretään kuvaaja, jossa näemme vihreällä heilurin kulman 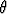sekä sinisellä kulmanopeuden

Heilurin kulma ajan funktiona muistuttaa kosinikäyrää. Tarkasteltu heilurin maksimiheilahduskulma on varsin suuri, jolloin approksimaation tarjoama differentiaaliyhtälön ratkaisu (esitetyillä alkuehdoilla) on huonohko. Kuitenkin modifioimalla ratkaisun taajuutta sopivalla kertoimella, saadaan heilurin värähtelylle varsin hyvä alkeisfunktioapproksimaatio.

Alla heilurin paikkaa (vihreä) approksimoidaan funktiolla (punainen katkoviiva).

Seuraavassa on muodostettu tarvittavat työkalut heilurin värähtelyn animoimiseksi. Värähtelevän heilurin lisäksi kuvassa näkyvät heilurin kuulaan vaikuttavat voimat. Varren tukivoima on punainen ja maan vetovoima sininen, vihreisiin osakomponentteihin jaettuna. Kyseessä on Mathematicalla kirjoitettu ohjelmakoodi.

Itse animaatio on lista peräkkäisiä kuvia, joka on ensin laskettava (kestää jonkin aikaa) ja sitten ajettava. Ajaminen tapahtuu napsauttamalla kuvasarjaa oikeassa reunassa yhdistävä hakanen aktiiviseksi (mustaksi) ja painamalla ctrl-y.

Entä mitä heilurille tapahtuu, jos sille annetaan hieman vauhtia? Tarkastellaan ensin tilannetta, jossa alkuehtoon lisätään vauhtia .

Numeerinen ratkaisu sievennyksineen.

Piirretään  jälleen kuvaaja, jossa vihreällä on heilurin kulma 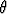sekä sinisellä kulmanopeus .

Alkeisfunktioiden tarjoamat ratkaisut eivät enää tunnu enää kovinkaan sopivilta. Animoidaan jälleen heilurin liikettä, jotta nähdään, mitä tapahtuu. Ensin muokataan hieman yllä käytettyä kuvankoodia.

Animaatiokuvat vievät runsaasti koneen muistia, joten muistin vapauttamiseksi voi olla hyvä poistaa edellinen animaatiokuvasarja ennen uuden laskemista. Tämä tapahtuu  napsauttamalla kuvasarjaa oikeassa reunassa yhdistävä hakanen aktiiviseksi (mustaksi) ja painamalla delete. Uusi animaatio.

Mitä heilurille tapahtuu kun vauhtia annetaan vielä enemmän? Kokeillaan alkuehtoa ja lasketaan.

Ja animointi vielä kerran.

Tarkastellaan seuraavaksi heilurien liikeratoja faasitasossa. Olkoon x-akselina heilurin liikkeen kulma ja y-akselina sen kulmanopeus. Ensimmäinen heiluriliike piirretään vihreällä, toinen sinisellä ja kolmas punaisella.

Tehtäviä

Heiluriliikkeet, jotka eivät tee kokonaisia pyörähdyksiä, muodostavat umpinaisen käyrän. Pyörivä heiluri muodostaa jatkuvan värähtelykäyrän. Mitä näillä faasitasokuvilla kuvataan?

Etsi heilurin alkuehtoja muokkaamalla heiluriliike, jossa heiluri juuri ja juuri pyörähtää ympäri. Mikä on lepoasennosta lähdettäessä tarvittava kulmanopeus? Miltä kyseinen liike näyttää faasitasossa?