Tykillä ampuminen 1

Heittoliikkeeseen kuuluu keskeisinä tekijöinä maan vetovoima sekä ilmanvastuksen aiheuttama nopeudelle vastakkaissuuntainen voima. Näitä voimia sovelletaan myös mallinnettaessa tykin ammuksen liikerataa.

Yksinkertaisimmassa mallissa jätetään ilmanvastus huomiotta. Tällöin ammukseen vaikuttaa lähtöhetken jälkeen vain maan vetovoima , missä on maan vetovoiman aiheuttama kiihtyvyys ja m ammuksen massa. Kun kiihtyvyys lausutaan derivaatan avulla , saa yleinen liikeyhtälö tällöin muodon

mistä massa m voidaan supistaa pois.

Tarkastellaan seuraavaa ongelmaa: Mikä on oikea ampumiskulma, kun 25 metrin korkeudella sijaitsevalta tykkilavetilta ammutaan 10 kg kranaatti nopeudella 500 m/s kohti meren pinnalla olevaa maalia, jonka etäisyys on tasan 10 km?

Jaetaan yllä esitetty toisen kertaluvun differentiaaliyhtälö kahteen eri osayhtälöön, z-suuntaan ja x-suuntaan, ja ratkaistaan yhtälöt. Laskujen aluksi on syytä hävittää mahdollisista aiemmista laskuista jääneet muuttujat.

> restart;

Määritellään differentiaaliyhtälöryhmä ja sen tuntemattomat muuttujat.

> ryhma:= diff(x(t), t$2)=0, diff(z(t), t$2)=-g;

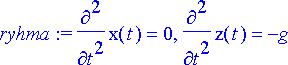
> muuttujat:= x(t), z(t);

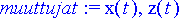
Määritellään vakiot ja alkuehto. Ammuksen lähtökulma olkoon 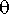. Sisällytetään ehtoon sekä ammuksen alkunopeus jaettuna nopeuskomponentteihin että lähtökorkeus.

> g:= 9.81: m:= 10: v0:= 500:

> alkuehto:= x(0)=0, z(0)=25, D(x)(0)=v0*cos(theta), D(z)(0)=v0*sin(theta);

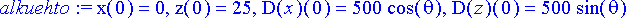
Ratkaistaan alkuarvoprobleema:

> dyrtk:= dsolve({ryhma, alkuehto}, {muuttujat});

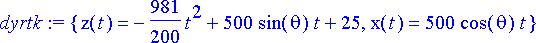
Ammuksen rata on paraabeli, jonka parametrimuotoinen esitys on

> lentorata:= subs(dyrtk, [x(t), z(t)]);

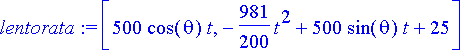
Ammuksen kokonaislentoaika ja lähtökulma saadaan ratkaisemalla yhtälöryhmä:

> sys:= zip((x, y)->x=y, lentorata, [10000, 0]);

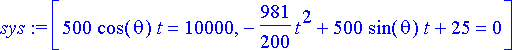
> rtk:= solve({sys[]}, {t, theta});

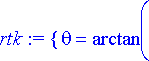
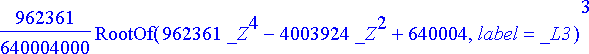
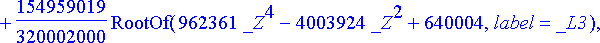
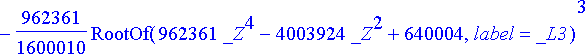
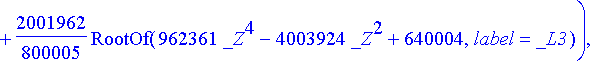
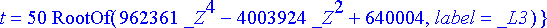
RootOf (...) edustaa jotakin yhtälön juurta. Juuret saadaan ratkaistua allvalues -komennolla.

> juuret:= [evalf(allvalues(rtk))];

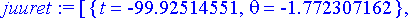
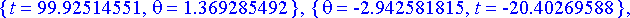
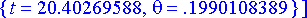
Vain positiiviset ratkaisut kelpaavat. Mahdollisuuksia on siis kaksi. Näitä vastaavat lentoradat ovat

> radat:= select(x->subs(x, t)>0, juuret);

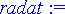
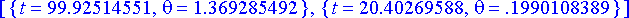
> rata1:= subs(theta=subs(radat[1], theta), lentorata);

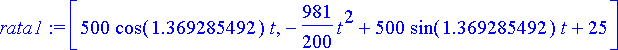
> rata2:= subs(theta=subs(radat[2], theta), lentorata);

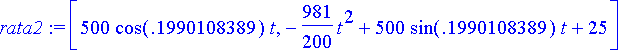
Sekunneissa ilmoitetut kokonaislentoajat ovat

> ajat:= map(x->subs(x, t), radat);

Lähtökulmat ovat radiaaneissa. Asteissa ilmoitettuina ne ovat

> map(x->subs(x, theta), radat):
evalf(map(x->convert(x, degrees), %));

Radoista voidaan piirtää kuvaajat ja yhdistää nämä samaan kuvaan:

> kuva1:= plot([rata1[], t=0..ajat[1]], color=green):
kuva1;

> kuva2:= plot([rata2[], t=0..ajat[2]], color=red):
kuva2;

> with(plots):

Warning, the name changecoords has been redefined

> display(kuva1, kuva2);

Tehtäviä

Määritä ampumaetäisyys lähtökulman funktiona. Piirrä funktion kuvaaja. Millä kulmalla saadaan suurin ampumaetäisyys? Mikä tämä etäisyys on? Kauanko ammuksen lento tällöin kestää?

Miten radan lakikorkeus riippuu lähtökulmasta? Entä ampumaetäisyydestä? Piirrä kuvaajat!