![[Maple Bitmap]](Images/tykki21.gif) , missä
, missä
![[Maple Bitmap]](Images/tykki22.gif) on maan vetovoiman aiheuttama kiihtyvyys ja
m
heitettävän kappaleen massa. Ilmanvastusvoima on verrannollinen nopeuden neliöön, ja se voidaan mallintaa lausekkeella
on maan vetovoiman aiheuttama kiihtyvyys ja
m
heitettävän kappaleen massa. Ilmanvastusvoima on verrannollinen nopeuden neliöön, ja se voidaan mallintaa lausekkeella
| tykki2.mws |
Mallinnettaessa heittoliikettä, kuten esimerkiksi tykillä ampumista, keskeisinä vaikuttavina tekijöinä ovat painovoima sekä ilmanvastuksen aiheuttama nopeudelle vastakkaissuuntainen voima.
Painovoima on
![[Maple Bitmap]](Images/tykki21.gif) , missä
, missä
![[Maple Bitmap]](Images/tykki22.gif) on maan vetovoiman aiheuttama kiihtyvyys ja
m
heitettävän kappaleen massa. Ilmanvastusvoima on verrannollinen nopeuden neliöön, ja se voidaan mallintaa lausekkeella
on maan vetovoiman aiheuttama kiihtyvyys ja
m
heitettävän kappaleen massa. Ilmanvastusvoima on verrannollinen nopeuden neliöön, ja se voidaan mallintaa lausekkeella
![[Maple Bitmap]](Images/tykki23.gif)
missä
b
on ilmanvastuskerroin,
v
skalaarinen nopeus,
![[Maple Bitmap]](Images/tykki24.gif) nopeus vektorina ja
nopeus vektorina ja
![[Maple Bitmap]](Images/tykki25.gif) nopeuden suuntainen yksikkövektori.
nopeuden suuntainen yksikkövektori.
Yleinen liikeyhtälö
![[Maple Bitmap]](Images/tykki26.gif) saa tällöin muodon
saa tällöin muodon
![[Maple Bitmap]](Images/tykki27.gif)
missä on merkitty
![[Maple Bitmap]](Images/tykki28.gif) sekä
sekä
![[Maple Bitmap]](Images/tykki29.gif) .
.
Tarkastellaan tilannetta, jossa tykillä ammutaan poispäin liikkuvaan maaliin. Mikä on oikea ampumiskulma, kun 25 metrin korkeudella sijaitsevalta tykkilavetilta ammutaan 10 kg kranaatti nopeudella 1000 m/s kohti maalia, jonka etäisyys ampumishetkellä on tasan 5 km? Maali liikkuu 15 m/s tykistä poispäin veden pintaa pitkin, ja ilmanvastuskerroin kranaatille on
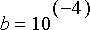 .
.
Jaetaan yllä esitetty toisen kertaluvun vektorimuotoinen differentiaaliyhtälö kahteen eri osayhtälöön, z-suuntaan ja x-suuntaan, ja ratkaistaan yhtälöt. Laskujen aluksi on syytä hävittää mahdollisista aiemmista laskuista jääneet muuttujat.
> restart;
Määritellään differentiaaliyhtälöryhmä ja sen tuntemattomat muuttujat.
> ryhma:= m*diff(x(t), t$2)=-b*diff(x(t), t)*sqrt(diff(x(t), t)^2+diff(z(t), t)^2), m*diff(z(t), t$2)=-m*g-b*diff(z(t), t)*sqrt(diff(x(t), t)^2+diff(z(t), t)^2);
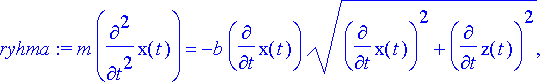
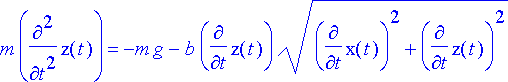
> muuttujat:= x(t), z(t);
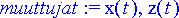
Määritellään vakiot ja alkuehto. Ammuksen lähtökulma olkoon
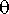 . Sisällytetään ehtoon sekä ammuksen alkunopeus jaettuna nopeuskomponentteihin että lähtökorkeus.
. Sisällytetään ehtoon sekä ammuksen alkunopeus jaettuna nopeuskomponentteihin että lähtökorkeus.
> g:= 9.81: b:= 10^(-4): m:= 10: v0:= 1000:
> alkuehto:= x(0)=0, z(0)=25, D(x)(0)=v0*cos(theta), D(z)(0)=v0*sin(theta);
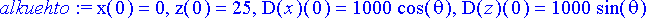
Differentiaaliyhtälöryhmä ei ole ratkaistavissa alkeisfunktioiden avulla, joten ryhmää ei voi ratkaista
Maple
n avulla
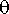 :n funktiona. Suljetussa muodossa olevan ratkaisun sijaan joudutaan turvautumaan arvaukseen. Arvataan jokin kulma (radiaaneissa), ja katsotaan, miten hyvin laukaus osui.
:n funktiona. Suljetussa muodossa olevan ratkaisun sijaan joudutaan turvautumaan arvaukseen. Arvataan jokin kulma (radiaaneissa), ja katsotaan, miten hyvin laukaus osui.
> theta:= 0.03;

> rtk1:= dsolve({ryhma, alkuehto}, {muuttujat}, numeric, startinit=true, output=listprocedure);
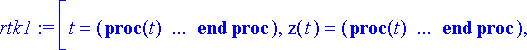
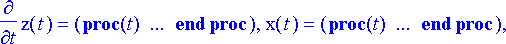
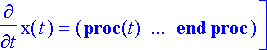
Poimitaan ratkaisusta x- ja z-suuntia kuvaavat komponentit listaksi ja piirretään kuvio.
> lentorata:= subs(rtk1, [x(t), z(t)]):
> plot([lentorata[], 0..10]);
![[Maple Plot]](Images/tykki221.gif)
Katsotaan miten lähelle laukaus osui. Huomaa, että ratkaisussa on huomioitu myös kohteen liike.
> lentoaika:= fsolve('lentorata[2](t)=0', t=0..10);
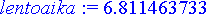
> osmaet:= lentorata[1](lentoaika)-(5000+15*lentoaika);
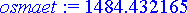
Ammus osuu veteen noin puolitoista kilometriä liian kauaksi. Lähtökulma oli siis liian suuri. Arvataan uudestaan tarkoituksena haarukoida oikea tulos arvausten väliin. Tämän jälkeen voidaan systemaattisesti hakea oikea kulma.
> theta:= 0.01;

> rtk2:= dsolve({ryhma,alkuehto}, {muuttujat}, numeric, startinit=true, output=listprocedure);
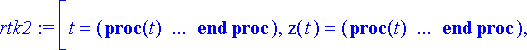
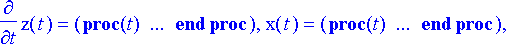
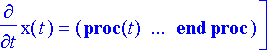
> lentorata:= subs(rtk2, [x(t), z(t)]):
> lentoaika:= fsolve('lentorata[2](t)=0', t=0..10);
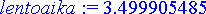
> osumaet:= lentorata[1](lentoaika)-(5000+15*lentoaika);
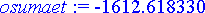
Nyt laukaus jäi liian lyhyeksi. Saimme kuitenkin haarukoitua osumisvälin. Löytääksemme tarkan ampumiskulman, teemme organisoidun kokeilun.
Tehdään pieni for -silmukka, joka tulostaa osumapaikan 21 laskupisteessä 0.001 radiaanin välein.
>
indeksi:= 0:
for theta from 0.01 by 0.001 to 0.03 do
rtk:= dsolve({ryhma, alkuehto}, {muuttujat}, numeric, startinit=true, output=listprocedure);
lentorata:= subs(rtk, [x(t), z(t)]);
lentoaika:= fsolve('lentorata[2](t)=0', t=0..10);
osumataul[indeksi]:= lentorata[1](lentoaika)-(5000+15*lentoaika);
kulmataul[indeksi]:= theta;
indeksi:= indeksi+1;
od:
kulmat:=[seq(kulmataul[k], k=0..20)]:
etaisyydet:= [seq(osumataul[k],k=0..20)];
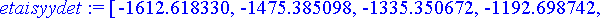
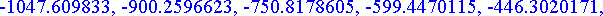
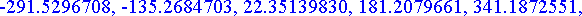
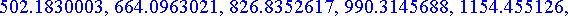
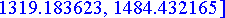
Etsitään lähintä osumaa vastaava indeksi ja tämän avulla ampumiskulma ja osumaetäisyys.
>
member(min(map(x->abs(x),etaisyydet)[]),etaisyydet,'ind'):
lahin:=[kulmat[ind],etaisyydet[ind]];
![lahin := [.21e-1, 22.35139830]](Images/tykki235.gif)
Sama uudestaan uudella kapeammalla haarukalla ja 0.0001 radiaanin askelvälillä.
>
indeksi:= 0:
for theta from 0.020 by 0.0001 to 0.022 do
rtk:= dsolve({ryhma, alkuehto}, {muuttujat}, numeric, startinit=true, output=listprocedure);
lentorata:= subs(rtk, [x(t), z(t)]);
lentoaika:= fsolve('lentorata[2](t)=0', t=0..10);
osumataul[indeksi]:= lentorata[1](lentoaika)-(5000+15*lentoaika);
kulmataul[indeksi]:= theta;
indeksi:= indeksi+1;
od:
kulmat:=[seq(kulmataul[k], k=0..20)]:
etaisyydet:= [seq(osumataul[k],k=0..20)];
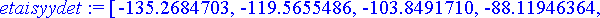
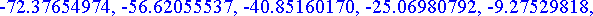
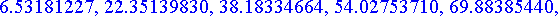
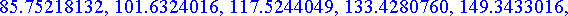
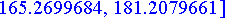
>
member(min(map(x->abs(x),etaisyydet)[]),etaisyydet,'ind'):
lahin:=[kulmat[ind],etaisyydet[ind]];
![lahin := [.209e-1, 6.53181227]](Images/tykki241.gif)
Osuma on siis runsaan kuuden metrin päässä ja vastaava ampumiskulma on asteissa
>
convert(lahin[1], degrees):
evalf(%);
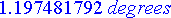
Piirrä lähimmäksi osuvan ammuksen lentorata. Määritä radan lakikorkeus ja ammuksen lentoaika.
Suurenna ilmanvastuskerrointa, ja tutki, miten se vaikuttaa radan muotoon.