Sovellukset : Populaatiomallit
Väestönkasvu
Populaation kehitystä voidaan usein kuvata differentiaaliyhtälöiden avulla. Tässä tarkastellaan yksinkertaista väestönkasvumallia, joka perustuu ihmispopulaation kehitykseen vakioympäristössä.
Kasvuyhtälö konstruoidaan seuraavalla logiikalla. Väestömäärän muutosta kuvaavaan yhtälöön vaikuttaa kaksi perustekijää,
syntyvyys
![s[0]](Images/vaestok11.gif) ja
kuolleisuus
ja
kuolleisuus
![k[0]](Images/vaestok12.gif) . Olkoon väestömäärää ajanhetkellä
t
kuvaava funktio
N
(
t
). Tällöin on voimassa differentiaaliyhtälö
. Olkoon väestömäärää ajanhetkellä
t
kuvaava funktio
N
(
t
). Tällöin on voimassa differentiaaliyhtälö
![diff(N(t),t) = (s[0]-k[0])*N(t)](Images/vaestok13.gif) ,
,
ts. väestömäärän muutosnopeus on verrannollinen senhetkiseen väestömäärään verrannollisuuskertoimena syntyvyyden ja kuolleisuuden erotus. Yhtälö ratkeaa helposti, jolloin saadaan väestömäärän kasvulle eksponentiaalinen malli
![N(t) = N[0]*exp(r*t)](Images/vaestok14.gif) ,
,
missä
![r = s[0]-k[0]](Images/vaestok15.gif) ja
ja
![N[0]](Images/vaestok16.gif) on populaation suuruus alkuhetkellä
on populaation suuruus alkuhetkellä
![t = t[0]](Images/vaestok17.gif) . Eksponentiaalinen kasvu kuvaa populaation kehitystä yleensä vain olosuhteissa, missä ympärisön asettamat rajoitukset ovat vähäiset ja populaation kasvupotentiaali rajaton.
. Eksponentiaalinen kasvu kuvaa populaation kehitystä yleensä vain olosuhteissa, missä ympärisön asettamat rajoitukset ovat vähäiset ja populaation kasvupotentiaali rajaton.
Tarkasteltaessa lähes mitä tahansa reaalista populaatiota, rajallinen ympäristö ja populaation itsensä aiheuttama lajin sisäinen kilpailu aiheuttavat kasvulle selkeät rajat. Kasvua rajoittava kilpailutekijä on yleensä kytketty populaatiotiheyteen. Niinpä ympäristön rajallista kantokykyä voidaan kuvata modifioimalla syntyvyyttä ja kuolleisuutta populaatiotiheyteen verrannollisella tekijällä. Tällöin
![diff(N,t) = N*(s[0]-p[s]*N-(k[0]+p[k]*N))](Images/vaestok18.gif) ,
,
missä
![p[s]](Images/vaestok19.gif) on populaatiotiheyden syntyvyyskerroin ja
on populaatiotiheyden syntyvyyskerroin ja
![p[k]](Images/vaestok110.gif) on populaatiotiheyden kuolleisuuskerroin.
on populaatiotiheyden kuolleisuuskerroin.
Kun populaatio saavuttaa maksimikokonsa
![N[max]](Images/vaestok111.gif) , sanotaan, että se on saavuttanut ympäristön kantokyvyn rajan. Tällöin derivaatta on = 0 ja populaatiolle pätee
, sanotaan, että se on saavuttanut ympäristön kantokyvyn rajan. Tällöin derivaatta on = 0 ja populaatiolle pätee
![N[max] = K](Images/vaestok112.gif) =
=
![(s[0]-k[0])/(p[s]+p[k])](Images/vaestok113.gif) .
.
Voidaan ajatella, että
K
on ympäristön kantokyky. Tällöin populaatiota koskeva differentiaaliyhtälö saa muodon
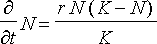
Tämä voidaan helposti todeta (aluksi poistetaan vanhat muuttujat varmuuden vuoksi):
>
restart;
>
subs({r=s[0]-k[0], K=(s[0]-k[0])/(p[s]+p[k])}, r*N*(K-N)/K):
simplify(%);
![-(-s[0]+k[0]+N*p[s]+N*p[k])*N](Images/vaestok115.gif)
Lasketaan seuraavaksi yksinkertainen populaatioesimerkki, missä alkukantainen heimo alkaa vuonna 1000 jkr. asuttaa Tyynen valtameren Kolae-saarta omaa vakiintunutta traditiotaan ja elämäntapaa soveltaen. Olkoon heimolle tyypillinen kasvukerroin
r
= 0.03 ja Kolae-saaren kantokyvyn raja
K
= 953 asukasta.
Heimon populaatiota kuvaava yhtälö on
>
yht:= diff(n(t), t)=r*n(t)*(k-n(t))/k;
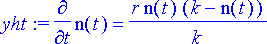
Valitaan alkuehto, joka kuvaa populaation kokoa asutuksen alkaessa.
>
alkuehto:= n(0)=10;
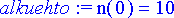
Ratkaistaan differentiaaliyhtälöryhmä.
>
dsolve({yht, alkuehto}, n(t)):
popul:= subs(%, n(t));
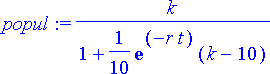
Sijoitetaan vakiot:
>
numpopul:= subs({r=0.03, k=953}, popul);
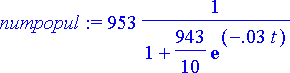
Piirretään kuva populaation kehityksestä ajan suhteen.
>
plot(numpopul, t=0..300, labels=["Aika/a", "Asukkaita"], title="Kolaen populaatio");
![[Maple Plot]](Images/vaestok120.gif)
Tuloksena on ns. s-kasvukäyrä, joka osoittaa saaren populaation vuonna 1300 jkr. jo varsin saturoituneeksi. Todellisuudessa vain harvoin ympäristöolot ovat niin tasaiset, että yllä lasketun kaltainen tasainen kasvukäyrä pääsisi syntymään. Tautiepidemiat, katovuodet yms. vaihtelevat tekijät muuttavat ympäristön kantokykyä ja kuolleisuustekijää merkittävästi jopa vuositasolla. Ihmispopulaatiossa lisäksi kehittyvä teknologia ja innovaatiot saattavat muuttaa ympäristötekijöiden vaikutuksia suuresti.
Tehtävä
Tarkastellaan tilannetta, missä heimon perinteet kannustaisivat jäseniä suurempiin perhekokoihin. Tällöin heimolle ominainen kasvukerroin onkin 4%. Kuinka monta vuotta kestää ennen kuin saaren asukasluku rikkoo 800 ihmisen rajan?
Sovelluksia: väestön kehitys muuttuvissa olosuhteissa
Sovelluksia: peto- ja saaliskanta
JP & SKK & MS 12.07.2001
![s[0]](Images/vaestok11.gif) ja
kuolleisuus
ja
kuolleisuus
![k[0]](Images/vaestok12.gif) . Olkoon väestömäärää ajanhetkellä
t
kuvaava funktio
N
(
t
). Tällöin on voimassa differentiaaliyhtälö
. Olkoon väestömäärää ajanhetkellä
t
kuvaava funktio
N
(
t
). Tällöin on voimassa differentiaaliyhtälö ![diff(N(t),t) = (s[0]-k[0])*N(t)](Images/vaestok13.gif) ,
,
![N(t) = N[0]*exp(r*t)](Images/vaestok14.gif) ,
,
![r = s[0]-k[0]](Images/vaestok15.gif) ja
ja
![N[0]](Images/vaestok16.gif) on populaation suuruus alkuhetkellä
on populaation suuruus alkuhetkellä
![t = t[0]](Images/vaestok17.gif) . Eksponentiaalinen kasvu kuvaa populaation kehitystä yleensä vain olosuhteissa, missä ympärisön asettamat rajoitukset ovat vähäiset ja populaation kasvupotentiaali rajaton.
. Eksponentiaalinen kasvu kuvaa populaation kehitystä yleensä vain olosuhteissa, missä ympärisön asettamat rajoitukset ovat vähäiset ja populaation kasvupotentiaali rajaton. ![diff(N,t) = N*(s[0]-p[s]*N-(k[0]+p[k]*N))](Images/vaestok18.gif) ,
,
![p[s]](Images/vaestok19.gif) on populaatiotiheyden syntyvyyskerroin ja
on populaatiotiheyden syntyvyyskerroin ja
![p[k]](Images/vaestok110.gif) on populaatiotiheyden kuolleisuuskerroin.
on populaatiotiheyden kuolleisuuskerroin.
![N[max]](Images/vaestok111.gif) , sanotaan, että se on saavuttanut ympäristön kantokyvyn rajan. Tällöin derivaatta on = 0 ja populaatiolle pätee
, sanotaan, että se on saavuttanut ympäristön kantokyvyn rajan. Tällöin derivaatta on = 0 ja populaatiolle pätee ![N[max] = K](Images/vaestok112.gif) =
=
![(s[0]-k[0])/(p[s]+p[k])](Images/vaestok113.gif) .
.
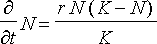
![-(-s[0]+k[0]+N*p[s]+N*p[k])*N](Images/vaestok115.gif)
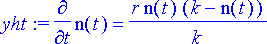
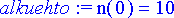
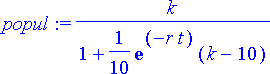
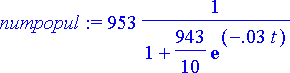
![[Maple Plot]](Images/vaestok120.gif)