Väestön kehitys muuttuvissa olosuhteissa

Populaation kehitystä voidaan usein kuvata differentiaaliyhtälöiden avulla.

Kun populaation ja ympäristön vaikutus on huomioitu, voidaan populaation kehitys kuvata differentiaaliyhtälöllä

,

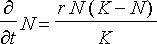missä N = N ( t ) on populaation suuruus tarkasteluhetkellä t , K on ympäristön kantokyky ja r on populaatiolle tyypillinen kasvukerroin. (Vrt. yksinkertaista väestönkasvua kuvaavaan esimerkkiin.)

Tarkastellaan tilannetta, missä vakiot K ja r muuttuvat ajan funktioina, eli

K = K( t ), r = r( t ).

Tämä vastaa tilannetta, missä ympäristötekijät ovat muutoksen alaisia. Esimerkiksi ihmispopulaation kyky hyödyntää ympäristöä voi muuttua tai ympäristön kantokyky ihmisen muokkauksen kautta muuntua. Kantokyky on myös syntyvyyden funktio!

Tyynen valtameren Kolae-saarta asuttavalle heimolle tyypillinen kasvukerroin olkoon 3%. Alkupopulaatio vuonna 1000 jkr. on 10 asukasta, mutta väestön kasvu ja heimon suosima veneiden rakentaminen sekä siitä aiheutuva puiden häviäminen johtavat eroosion kiihtymiseen saarella ja saaren alkuperäisen kantokyvyn romahtamisen. Nyt kantokykyä kuvataan seuraavassa esitettävällä funktiolla, jossa kantokyky laskee väestömäärän kasvaessa ja ajan kuluessa.

Tarkastellaan Kolae-saaren väestön kehittymistä 500 vuoden ajanjakson verran.

Aluksi poistetaan vanhat muuttujat.

> restart;

Määritellään kantokykyfunktio K ja piirretään sille kuvaaja.

> k:= t->953*exp(-n(t)*0.000005*t+0.0005);

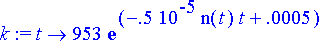
> plot3d(subs(n(t)=n, k(t)), t=0..500, n=0..953, axes=boxed, orientation=[-60,20], labels=["Vuosia", "Väkiluku", "Kantokyky"]);

Lyhyillä aikaväleillä käyttäytyminen on lähes lineaarisesti laskeva, vaikka pidemmillä tarkasteluväleillä kantokyvyn eksponentiaalinen vähentyminen tulee esille. Mallilla pyritään osoittamaan mekanismi, joka alkuun päästyään aiheuttaa pitkällisen vaikutuksen.

Kasvukerroinfunktio r olkoon vakio:

> r:= t->0.03;

Populaatiota kuvaava differentiaaliyhtälö on tällöin

> yht:= diff(n(t), t)=r(t)*n(t)*(k(t)-n(t))/k(t);

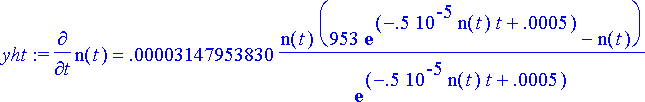
Alkuehto, joka kuvaa populaation kokoa asutuksen alkaessa:

> alkuehto:= n(0)=10;

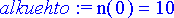
Ratkaistaan differentiaaliyhtälöryhmä numeerisesti.

> dsolve({yht, alkuehto}, n(t), type=numeric, output=listprocedure):
popul:= subs(%, n(t));

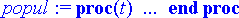
Piirretään kuvaaja väestön kehitykselle.

> plot(popul, 0..500, labels=["Aika/a", "Asukkaita"], title="Kolaen populatio", view=[0..500, 0..1000]);

Tuloksena ei olekaan säännöllinen s-käyrä, vaan noin 150 vuoden kohdalla populaation kehityksessä tapahtuu muutos. Eroosio on vaikuttanut ympäristön kantokykyä alentavasti niin, että väestönkasvu pysähtyy. Eroosio kuitenkin yhä jatkuu, mikä aiheuttaa kantokyvyn heikkenemisen jatkumisen ja siten heimon väestön vähentymisen.

Myös tautiepidemiat voivat muuttaa merkittävästi populaation kasvukerrointa. Kasvukerroin r voisi muuttua esimerkiksi kuolleisuutta voimakkaasti lisäävän tautiepidemian seurauksena seuraavasti

,

missä = 0.03. Piirretään kasvukertoimen kuvaaja.

> r:= t->0.03*(1-1.7*(tanh((t-200)/20)-tanh((t-240)/20)));

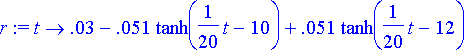
> plot(r, 0..500, view=[0..500, -0.05..0.04]);

Tehtäviä

Yllä esitetyllä tavalla populaation kasvukerrointa muuttava tautiepidemia iskee Kolae-saaren heimoon. Oletetaan, että kantokyky on vakio K = 953, ts. ei huomioida eroosiota, ainoastaan tauti. Kuinka tautiepidemia vaikuttaa populaation kehitykseen? Piirrä kuvaaja Kolae-saaren väkiluvulle 500 vuotta alkuasutuksesta eteenpäin. Vertaa tulostasi 'Väestönkasvu'-esimerkin tuloksiin.

Tarkastele myös populaation kehitystä, kun huomioit sekä Kolae-saaren heimoon iskevän taudin että ympäristön eroosion vaikutuksen yhdessä. Mikäli ottaisit myös huomioon heimon kehittämän uuden, tehokkaamman maanviljelymenetelmän, mihin tekijään se vaikuttaisi?