
| laji | 1. päivä | 2. päivä | 3. päivä |
| A | 112 | 133 | 91 |
| B | 35 | 49 | 28 |
Neljäntenä päivänä lukumäärät ovat samat kuin ensimmäisenä, viidentenä samat kuin toisena jne. On luonnollista olettaa, että syntyvien toukkien lukumäärä on suoraan verrannollinen lajin aikuisten määrään. Lisäksi tiedetään, että B-lajin aikuiset syövät A-lajin toukkia. Tällöin (kun tarkastellaan A- ja B-lajin aikuisten lukumääriä An ja Bn eri sukupolvissa n) voidaan ajatella, että peräkkäisissä sukupolvissa A-lajin aikuisten lukumäärät noudattavat mallia
An+1 = aAn + bBn (n = 1, 2, . . . ).
Toteuttaako havaintoaineisto mallin, ts. voidaanko vakiot a ja b valita siten, että malli on yhteensopiva havaintoaineiston kanssa? Minkä tiedon vakio b sisältää? Voidaanko B-lajin aikuisten lukumäärien vaihtelua selittää vastaavasti mallillaBn+1 = cBn + dAn?

Kahdesta ensimmäisestä yhtälöstä saadaan vakioiksi a = 4 ja b = -9. Kolmas yhtälö toteutuu, kun nämä sijoitetaan siihen. Johtopäätös on, että malli (1) on yhteensopiva havaintoaineiston kanssa. Vakio b = -9 merkitsee, että kukin B-lajin aikuinen syö (keskimäärin) 9 A-lajin toukkaa.
Sijoittamalla havaintoarvot malliin (2) Bn+1 = cBn + dAn saadaan yhtälöryhmä

Kahdesta ensimmäisestä yhtälöstä c = - ja d =
ja d = 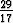 . Sijoitus kolmanteen yhtälöön antaa
ristiriidan
. Sijoitus kolmanteen yhtälöön antaa
ristiriidan  = 35. Malli (2) ei siten ole yhteensopiva havaintojen kanssa.
= 35. Malli (2) ei siten ole yhteensopiva havaintojen kanssa.
| Piilota ratkaisu |