 +
+  = -
= - x +
x + 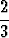
Kolme poikaa on saanut tehtäväksi työntää kahdet samanlaiset kärryt 2 km matkan. Kunkin pojan kävelynopeus ilman kärryä on 7 km/h ja kärryä työntäen 3 km/h. Kaksi poikaa yhdessä työntää yhtä kärryä nopeudella 6 km/h. Määritä lyhin aika, jossa pojat voivat yllämainittuja nopeuksia käyttäen selviytyä tehtävästä, kun enintään kaksi poikaa yhdessä työntää yhtä kärryä eikä kukaan työnnä kahta kärryä yhtä aikaa.
Kärryn 1 kuljetusaika t1(x):
A ja C työntävät yhdessä matkan x, jonka jälkeen A jatkaa yksin loppumatkan 2 - x.
t1(x) =  +
+  = -
= - x +
x + 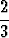
Kärryn 2 kuljetusaika t2(x):
Ajassa  poika B on edennyt matkan
poika B on edennyt matkan  . 3 =
. 3 = 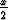 , joten poikien B ja C välimatka
pojan C lähtiessä paluumatkalle on x -
, joten poikien B ja C välimatka
pojan C lähtiessä paluumatkalle on x -  =
=  . B etenee nopeudella 3 km/h ja C
nopeudella 7 km/h, joten he kohtaavat ajan
. B etenee nopeudella 3 km/h ja C
nopeudella 7 km/h, joten he kohtaavat ajan  kuluttua. Poika B on siis ehtinyt
yksinään työntää kärryä ajan
kuluttua. Poika B on siis ehtinyt
yksinään työntää kärryä ajan 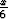 +
+  =
=  x. Pojat työntävät yhdessä loppumatkan
2 -
x. Pojat työntävät yhdessä loppumatkan
2 -  x . 3 = 2 -
x . 3 = 2 -  x.
x.
t2(x) = 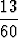 x +
x +  =
=  x +
x + 
Tehtävänä on siis etsiä minimi funktiolle
f(x) = max {t1(x), t2(x)},
missä 0 < x < 2.
|
- x +
x +  =
=  x +
x + 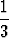 .
.
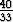 . Lyhin aika, joka kuluu kärryjen työntämiseen perille on
t1 (
. Lyhin aika, joka kuluu kärryjen työntämiseen perille on
t1 ( ) =
) =  eli 27 minuuttia ja 53 sekuntia.
eli 27 minuuttia ja 53 sekuntia.
| Piilota ratkaisu |