
Polkupyöräilijä, joka ajaa lokasuojattomalla maastopyörällä märkää vaakasuoraa tietä pitkin, voi likaantua selästään takapyörän heittämän kuran johdosta. Tarkastelemme ongelmaa pyörän mukana liikkuvassa (x, y)-kordinaatistossa, jonka x-akseli osoittaa ajosuuntaan. Olkoon v ajonopeus (vakio) ja R takapyörän säde. Newtonin liikelakien mukaan takapyörästä hetkellä t = 0 irtoavan kurapisaran lentoradan pisteet (x, y) = (x(t), y(t)), t > 0 (ajan t yksikkö s), toteuttavat ehdot

 kulma joka ilmoittaa kurapisaran satunnaisesti
vaihtelevan irtoamiskohdan.
kulma joka ilmoittaa kurapisaran satunnaisesti
vaihtelevan irtoamiskohdan.
Merkitsemme a = gR/v2 ja p = cos  . Näytä, että jos 0 < p < 1, niin kurapisaran
lentorata kulkee pisteen (0, H) kautta, missä
. Näytä, että jos 0 < p < 1, niin kurapisaran
lentorata kulkee pisteen (0, H) kautta, missä
H = R[ a + p-1 -
a + p-1 - 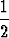 ap-2].
ap-2].
On näytettävä, että jos x(t) = 0, niin y(t) = H.
Jos x(t) = 0, niin t =  ; sijoittamalla tämä sekä tehtävässä annetut a ja p
saadaan
; sijoittamalla tämä sekä tehtävässä annetut a ja p
saadaan
y(t) = Rcos  + vtsin
+ vtsin  -
-  gt2 = . . . = R(
gt2 = . . . = R( +
+ 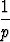 -
- 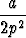 ) = H.
) = H. ![[]](kuvat/msam10-c-3.gif)
| Piilota ratkaisu |