| A = ”nopan silmäluku muu kuin 1” |
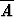 = ”nopan silmäluku on 1”. = ”nopan silmäluku on 1”. |
| A = ”nopan silmäluku muu kuin 1” |
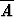 = ”nopan silmäluku on 1”. = ”nopan silmäluku on 1”. |
 .
.
Tämän perusteella saadaan
P (10 heiton sarjassa ei esiinny yhtään ykköstä) = P (A)10
ja komplementtitapahtuman todennäköisyydeksi
| P (10 heiton sarjassa esiintyy ainakin yksi ykkönen) |
| = 1 - P (10 heiton sarjassa ei esiinny yhtään ykköstä) |
| = 1 - P (A)10 . |
E(x) = P (A)10 . 10000 + (1 - P (A)10) . (-2000)  -62 (mk).
-62 (mk).
| Piilota ratkaisu |