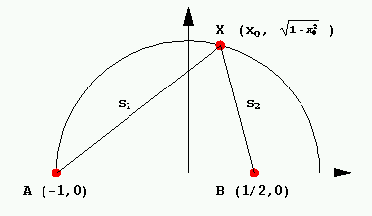
 (-1 < x < 1). Tulipalon
sattuessa pisteessä B = (
(-1 < x < 1). Tulipalon
sattuessa pisteessä B = ( , 0) paloauto kiitää nopeudella 100 km/h suoraan joen
kohtaan X, jossa auton vesisäiliö täytetään. Tämän jälkeen auto jatkaa matkaansa
suoraan kohti palopaikkaa nopeudella 45 km/h. Miten piste X on valittava, jotta
paloauto vesisäiliö täytettynä ehtisi palopaikalle mahdollisimman lyhyessä ajassa?
, 0) paloauto kiitää nopeudella 100 km/h suoraan joen
kohtaan X, jossa auton vesisäiliö täytetään. Tämän jälkeen auto jatkaa matkaansa
suoraan kohti palopaikkaa nopeudella 45 km/h. Miten piste X on valittava, jotta
paloauto vesisäiliö täytettynä ehtisi palopaikalle mahdollisimman lyhyessä ajassa? | matka joelle | = | s1 | ||
| matka joelta palopaikalle | = | s2 | ||
| nopeus matkalla joelle | = | v1 | = | 100 km/h |
| nopeus matkalla palopaikalle | = | v2 | = | 45 km/h |
| aika matkalla joelle | = | t1 | ||
| aika matkalla palopaikalle | = | t2 | ||

|
 ) vastaavasti em. pisteen
sekä pisteen (
) vastaavasti em. pisteen
sekä pisteen (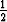 , 0) välisinä etäisyyksinä:
, 0) välisinä etäisyyksinä:
| s1 | = |  | = | 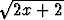 |
| s2 | = | 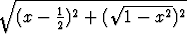 | = |  . . |
t(x) =  +
+  (-1 < x < 1) ,
(-1 < x < 1) ,
Funktion derivaatan lauseke on
| t'(x) | = |   + +   |
| = |  - -  |
|
| = |  |
|
90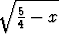 | = | 100 |
8100( - x) - x) | = | 10000(2x + 2) |
| x | = | - . . |
t(- ) ) |  0.0395 0.0395 |
| t(-1) |  0.0333 0.0333 |
| t(1) |  0.0311 0.0311 |
| Piilota ratkaisu |