Pullon piilotusta
Insinööriosastojen valintakoetehtävä vuodelta 1997
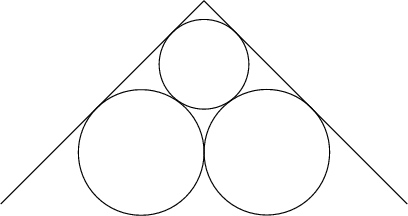
Jeppe Niilonpoika on löytänyt
pullolleen hienon piilopaikan hyllyn suorakulmaisesta nurkasta kahden suuren
sylinterinmuotoisen maalipurkin takaa. Kuinka suuri voi täysin näkymättömissä olevan
pullon halkaisija d enintään olla, kun kummankin maalipurkin halkaisja on (tarkasti) 2
dm?
Ilmoita pullon halkaisijan tarkka arvo (desimetreissä) ja likiarvo millimetreissä yhden
yksikön tarkkuudella.
Vihje 1
Tehtävässä on laskettava pullon ja purkin keskipisteiden välinen etäisyys ja
pääteltävä siitä purkin halkaisijan avulla pullon säde.
Vihje 2
Purkkien leikkauspiste, pullon keskipiste ja purkin keskipiste muodostavat
suorakulmaisen kolmion, jonka hypotenuusa halutaan laskea. Hypotenuusan laskemiseksi
Pythagoraan lauseen avulla on toinenkin kateetti tunnettava.
Vihje 3
Etäisyys purkkien leikkauspisteestä nurkkaan on sama kuin etäisyys
leikkauspisteestä toisen purkin keskipisteen kautta seinään.
Vihje 4
Edellisen vihjeen suora, purkin keskipisteestä piirretty suora purkin ja seinän
leikkauspisteeseen, sekä seinä muodostavat tasakylkisen kolmion. Tämän kolmion avulla
saadaan laskettua etäisyys purkkien leikkauspisteestä purkin keskipisteen kautta
seinään.
Pullon keskipisteen etäisyys taas saadaan ilmaistua r:n avulla.
Ratkaistaessa r toisen asteen yhtälöstä on mietittävä, mitä eri vastaukset tarkoittavat.