| 1. pompussa |  m(v m(v )2, )2, |
| 2. pompussa |  m(v m(v )2 = 0.95 . )2 = 0.95 .  m(v m(v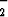 )2 = 0.95 . )2 = 0.95 .  m(v m(v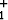 )2, )2, |
 | |
| n. pompussa |  m(v m(v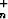 )2 = (0.95)n-1 . )2 = (0.95)n-1 .  m(v m(v )2, )2, |
 ja kimmahdusnopeus lattiasta v
ja kimmahdusnopeus lattiasta v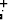 ,
voidaan olettaa (kun ilmanvastus jätetään ottamatta huomioon), että v
,
voidaan olettaa (kun ilmanvastus jätetään ottamatta huomioon), että v = v
= v ja että ti+1 - ti = kv
ja että ti+1 - ti = kv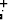 , missä k on vakio. Laske, kuinka kauan pallo pomppii
ajanhetken t1 jälkeen, kun jokaisessa lattiaan törmäyksessä pallo menettää 5 %
liike-energiastaan ja kun ensimmäinen pomppu kestää ajan t2 - t1 = 0.6 s. Ilmoita vastaus
sekunteina yhden desimaalin tarkkuudella. (Liike-energian kaava on E =
, missä k on vakio. Laske, kuinka kauan pallo pomppii
ajanhetken t1 jälkeen, kun jokaisessa lattiaan törmäyksessä pallo menettää 5 %
liike-energiastaan ja kun ensimmäinen pomppu kestää ajan t2 - t1 = 0.6 s. Ilmoita vastaus
sekunteina yhden desimaalin tarkkuudella. (Liike-energian kaava on E = 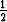 mv2.)
mv2.) | 1. pompussa |  m(v m(v )2, )2, |
| 2. pompussa |  m(v m(v )2 = 0.95 . )2 = 0.95 .  m(v m(v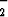 )2 = 0.95 . )2 = 0.95 .  m(v m(v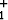 )2, )2, |
 | |
| n. pompussa |  m(v m(v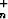 )2 = (0.95)n-1 . )2 = (0.95)n-1 .  m(v m(v )2, )2, |
joten yleisesti
v = v
= v (
( )n-1, n = 1, 2, . . .
)n-1, n = 1, 2, . . .
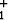 = 0.6, saadaan n. pomppuun kuluvaksi
ajaksi
= 0.6, saadaan n. pomppuun kuluvaksi
ajaksi
tn+1 - tn = kv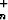 = kv
= kv (
( )n-1 = 0.6(
)n-1 = 0.6( )n-1.
)n-1.
0.6 + 0.6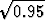 + 0.6(
+ 0.6(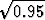 )2 + . . . =
)2 + . . . = 
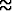 23.7s.
23.7s.
| Piilota ratkaisu |