Valokeila
Arkkitehtiosastojen valintakoetehtävä vuodelta 1993
Tehokkaalla valonheittimellä, jonka
valokeila oletetaan kartion muotoiseksi, valaistaan tasaista maastoa h metriä korkeasta
tornista. Maastoon syntyy valaistu alue, jonka tornia lähin piste on a metrin
etäisyydellä tornista. Asetetaan xyz-koordinaatisto siten, että maan pinta on xy-tasolla
ja että valonlähde on pisteess (0, 0, h). Määritä valaistun alueen reunaviivan
yhtälö xy-koordinaattitasossa, kun valokartion akseli on y-akseli suuntainen.
Ratkaisu
Piirtämällä xyz-koordinaatistoon kartio, jonka huippu on pisteessä (0, 0, h) ja akseli
y-akselin suuntainen, havaitaan, että kartion vaippa leikkaa xy-tason käyrää viivaa
pitkin.
Olkoon A = (0, 0, h), B = (0, a, 0), C = (0, a, h), D = (x, y, 0) ja E = (0, y, h). Näistä piste
D on tarkasteltavan käyrän mielivaltainen piste xy-tasossa. Koska suorat AB ja AD ovat
kartion vaipalla, on 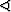 BAC =
BAC = 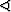 DAE. Näiden kulmien tangenttifunktion arvot myös
yhtyvät, jolloin
DAE. Näiden kulmien tangenttifunktion arvot myös
yhtyvät, jolloin
 =
= 
eli
 -
-  = 1 (hyperbeli).
= 1 (hyperbeli).


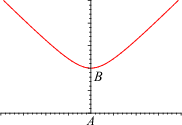
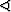 BAC =
BAC =  DAE. Näiden kulmien tangenttifunktion arvot myös
yhtyvät, jolloin
DAE. Näiden kulmien tangenttifunktion arvot myös
yhtyvät, jolloin
 =
= 
 -
-  = 1 (hyperbeli).
= 1 (hyperbeli).