Vesikourun suunnittelu
Kevään pitkän matematiikan ylioppilastehtävä vuodelta 1990
Vesikourun poikkileikkaus
A on alla olevan kuvion mukainen. Virtausvastuksen pienentämiseksi a + 2b
pyritään saamaan mahdollisimman pieneksi. Määritä vastaavat a ja b millimetrin
tarkkuudella.
Ratkaisu
Kuviossa annettujen tietojen perusteellla puolisuunnikkaan korkeus on  , sillä
puolisuunnikkaaseen voidaan muodostaa tasakylkiset suorakulmaiset kolmiot, joiden
terävät kulmat ovat 45o ja hypotenuusa b.
Tämän perusteella puolisuunnikkaan yhdensuuntaiset sivut ovat a ja a + 2 .
, sillä
puolisuunnikkaaseen voidaan muodostaa tasakylkiset suorakulmaiset kolmiot, joiden
terävät kulmat ovat 45o ja hypotenuusa b.
Tämän perusteella puolisuunnikkaan yhdensuuntaiset sivut ovat a ja a + 2 .  sekä
korkeus
sekä
korkeus 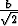 , joten pinta-alaehdon perusteella saadaan yhtälö
, joten pinta-alaehdon perusteella saadaan yhtälö
 .
.  = 15.
= 15.
Tästä yhtälöstä voidaan ratkaista esimerkiksi a:
a =  -
-  (1).
(1).
Optimoitava lauseke voidaan palauttaa yhtälön (1) avulla yhden muuttujan lausekkeeksi,
jota merkitään jatkossa f(b), seuraavasti
a + 2b =  -
-  + 2b =
+ 2b =  + (2 -
+ (2 - 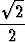 )b,
)b,
missä b  ]0,
]0,  [.
[.
Pienimmään arvon löytämiseksi tutkitaan funktion f derivaatan nollakohtia:
f'(b) = 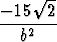 + 2 -
+ 2 -  =
=  (2),
(2),
joka on yhtä suuri kuin nolla, kun
b = 

 4.0506 dm.
4.0506 dm.
Kyseessä on minikohta, sillä lausekkeen (2) osoittaja on ylöspäin aukeava paraabeli,
jonka huippu löytyy derivaatan nollakohdasta. Nimittäjä on tarkasteluvälillä
positiivinen.
Lausekkeesta (1) voidaan laskea a 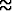 2.3728 dm.
2.3728 dm.


 , sillä
puolisuunnikkaaseen voidaan muodostaa tasakylkiset suorakulmaiset kolmiot, joiden
terävät kulmat ovat 45o ja hypotenuusa b.
, sillä
puolisuunnikkaaseen voidaan muodostaa tasakylkiset suorakulmaiset kolmiot, joiden
terävät kulmat ovat 45o ja hypotenuusa b.

 sekä
korkeus
sekä
korkeus 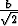 , joten pinta-alaehdon perusteella saadaan yhtälö
, joten pinta-alaehdon perusteella saadaan yhtälö
 .
.  = 15.
= 15.
 -
-  (1).
(1).
 -
-  + 2b =
+ 2b =  + (2 -
+ (2 - 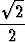 )b,
)b,
 ]0,
]0,  [.
[.
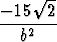 + 2 -
+ 2 -  =
=  (2),
(2),


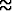 4.0506 dm.
4.0506 dm.
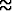 2.3728 dm.
2.3728 dm.