1 Logiikan ja joukko-opin alkeet
1.1 Logiikkaa
Tehtävä 1
Osoita totuusarvotauluja käyttäen, että implikaatio p q voidaan kirjoittaa
muotoon ¬p
q voidaan kirjoittaa
muotoon ¬p 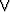 q, ts. että propositio (p
q, ts. että propositio (p  q)
q) 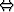 (¬p
(¬p 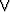 q) on identtisesti tosi.
q) on identtisesti tosi.
Tehtävä 2
Todista totuusarvotauluja käyttäen loogiset de Morganin lait: a) ¬(p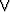 q)
q) 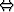 (¬p
(¬p  ¬q), b) ¬(p
¬q), b) ¬(p  q)
q) 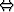 (¬p
(¬p 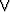 ¬q).
¬q).
Tehtävä 3
Todista totuusarvotaulua käyttäen konjunktiivinen distributiivisuus: [p (q
(q 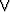 r)]
r)] 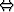 [(p
[(p  q)
q) 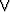 (p
(p  r)].
r)].
Tehtävä 4
Lausu propositiot p q ja p
q ja p 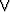 q käyttäen yksinomaan negaatiota ja
implikaatiota (mutta ei konjunktiota tai disjunktiota).
q käyttäen yksinomaan negaatiota ja
implikaatiota (mutta ei konjunktiota tai disjunktiota).
Tehtävä 5
Looginen NAND-operaatio p|q määritellään totuusarvotaululla| p | q | p|q | ||
| 1 | 1 | 0 | ||
| 1 | 0 | 1 | ||
| 0 | 1 | 1 | ||
| 0 | 0 | 1 | ||
Osoita: a) p|p 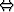 ¬p, b) (p|p)|(q|q)
¬p, b) (p|p)|(q|q) 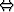 p
p 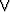 q, c) (p|q)|(p|q)
q, c) (p|q)|(p|q) 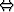 p
p  q.
q.
Tehtävä 6
Mitkä seuraavista reaalilukua x koskevista väittämistä ovat tosia, mitkä eivät?
a) 2x > 3  x > 2, b) 3x < 4
x > 2, b) 3x < 4  x < 1
x < 1 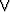 2x < 3, c) ¬(x > 1
2x < 3, c) ¬(x > 1 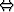 x > 0
x > 0  x > 1).
x > 1).
Tehtävä 7
Olkoot x ja y reaalilukuja, x > 0, y > 0. Ovatko seuraavat väittämät tosia?
a) 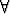 x
x 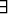 y (y < x), b)
y (y < x), b) 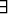 x
x 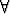 y (y > x).
y (y > x).
Tehtävä 8
Olkoot x ja reaalilukuja. Ovatko seuraavat propositiot tosia:
reaalilukuja. Ovatko seuraavat propositiot tosia:
a) 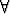 (
( > 0)
> 0) 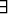 (x
(x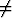 1) (|x - 1| <
1) (|x - 1| <  ), b)
), b) 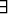 (x
(x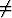 1)
1) 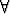 (
( > 0) (|x - 1| <
> 0) (|x - 1| <  ) ?
) ?
Tehtävä 9
Funktion f :

 (
( = reaaliluvut) jatkuvuus määritellään ehdolla
= reaaliluvut) jatkuvuus määritellään ehdolla
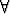 (
( > 0)
> 0) 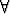 (x
(x 
 )
) 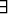 (
(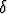 > 0)
> 0) 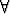 (y
(y 
 ) (|y - x| <
) (|y - x| < 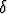
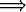 |f(y) - f(x)| <
|f(y) - f(x)| <  ).
).
Ns. tasainen jatkuvuus taas määritellään ehdolla
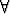 (
( > 0)
> 0) 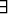 (
(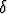 > 0)
> 0) 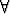 (x
(x 
 )
) 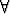 (y
(y 
 ) (|y - x| <
) (|y - x| < 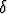
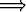 |f(y) - f(x)| <
|f(y) - f(x)| <  ).
).
Selosta, mikä ero näillä käsitteillä on.
1.2 Matemaattisesta todistamisesta
Tehtävä 10
Osoita totuusarvotauluja käyttäen propositiot
[p  (p
(p  q)]
q)]  q ja [p
q ja [p  (¬q
(¬q  ¬p)]
¬p)]  q
q
tautologioiksi. Millaisia matemaattisia todistustapoja nämä säännöt vastaavat?
Tehtävä 11
Olkoon n luonnollinen luku. Todista: n on parillinen, jos ja vain jos n2 on parillinen. Selosta todistuksen looginen rakenne.Tehtävä 12
Tarkoittakoon a jotakuta teekkaria ja olkoon p propositio ’a Ø’ (Ø on tyhjä
joukko). Olkoon q propositio ’a on vihreäsilmäinen leijona’. Onko propositio p
Ø’ (Ø on tyhjä
joukko). Olkoon q propositio ’a on vihreäsilmäinen leijona’. Onko propositio p  q tosi
vai epätosi? Jos propositio on tosi, niin seuraako tästä, että kaikki teekkarit ovat leijonia?
q tosi
vai epätosi? Jos propositio on tosi, niin seuraako tästä, että kaikki teekkarit ovat leijonia?
1.3 Joukko-oppia
Tehtävä 13
Olkoon
A = { n 
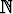 | 280/n
| 280/n 
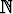 }, B = { 2n+1 | n
}, B = { 2n+1 | n 
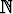 }, C = { x
}, C = { x 
 | 0 < x < 10 } = ]0, 10[.
| 0 < x < 10 } = ]0, 10[.
Määritä a) A  B, b) A
B, b) A  C, c) B
C, c) B  C, d) A
C, d) A 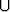 C, e) (A
C, e) (A 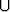 B)
B)  C, f) (B
C, f) (B 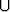 C)
C)  A.
A.
Tehtävä 14
Todista:| a) | A 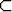 B B   A A 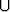 B = B B = B   A A  B = A, B = A, | ||
| b) | A 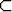 B B  A A 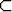 C C   A A 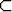 B B  C, C, | ||
| c) | A 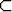 C C  B B 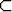 C C   A A 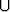 B B 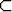 C, C, | ||
| d) | A 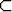 B B   A A  C C 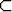 B B  C C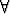 C. C. |
Tehtävä 15
Todista joukko-opilliset de Morganin lait. Piirrä kuviot.Tehtävä 16
Olkoot A ja B joukkoja. Todista:
(A 
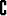 B)
B) 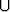 B = (A
B = (A 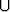 B)
B) 
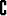 B
B 
 B = Ø.
B = Ø.
Tehtävä 17
Olkoot A, B ja C saman perusjoukon osajoukkoja. Todista identiteetit| a) | (A  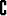 B) B)  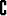 C = A C = A  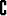 (B (B 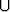 C), C), | ||
| b) | A  (B (B  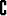 C) = (A C) = (A  B) B)  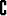 (A (A  C), C), | ||
| c) | (A  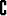 B) B) 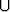 (A (A  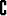 C) = A C) = A  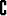 (B (B  C), C), | ||
| d) | (A  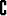 B) B)  (A (A  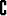 C) = A C) = A  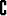 (B (B 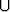 C) C) |
1o tutkimalla mielivaltaisen alkion x kuulumista oikean ja vasemman puolen joukkoihin, 2o soveltamalla joukkoalgebran laskusääntöjä. Piirrä kuviot joukoista.
Tehtävä 18
Olkoon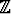 kaikkien kokonaislukujen joukko. Todista:
a) { 3n + 2 | n
kaikkien kokonaislukujen joukko. Todista:
a) { 3n + 2 | n 
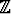 } = { 3n - 7 | n
} = { 3n - 7 | n 
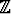 }, b) { 7n + 3 | n
}, b) { 7n + 3 | n 
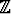 } = { 7n - 32 | n
} = { 7n - 32 | n 
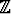 }.
}.
Tehtävä 19
Sievennä joukko-opilliset lausekkeet
a) 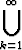 [-1 +
[-1 + 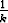 , 1 -
, 1 - 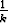 ], b)
], b) 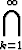 ] -
] - 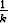 ,
, 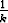 [.
[.
Tehtävä 20
Olkoon
A = { (x, y) | (x - cos
= { (x, y) | (x - cos  )2 + (y - sin
)2 + (y - sin  )2 < 4 }
)2 < 4 }
xy-tason joukko. Millainen joukko on
![/~\
f (- [0,2p]](kuvat/ag10x.gif) A
A ?
?
Tehtävä 21
Olkoot A, B ja C saman perusjoukon joukkoja. Todista, että (A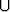 B) × C = (A × C)
B) × C = (A × C) 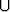 (B × C).
(B × C).
Tehtävä 22
Olkoot reaaliluku x relaatiossa R reaalilukuun y, jos x < 1/y. Millainen karteesisen tulon ×
×  osajoukko relaatio R on?
osajoukko relaatio R on?
Tehtävä 23
Olkoot luonnolliset luvut n ja m relaatiossa P toisiinsa, jos n2 + m2 on luonnollisen luvun neliö. Piirrä kuva relaatiosta P karteesisen tulon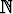 ×
× 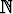 osajoukkona;
tarkastele arvoja n, m < 20.
osajoukkona;
tarkastele arvoja n, m < 20.
1.4 Kuvaus
Tehtävä 24
Etsi mahdollisimman laaja lähtöjoukko reaalimuuttujan x reaaliarvoiselle funktiolle
f(x) = 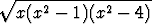 .
.
Tehtävä 25
Määritä mahdollisimman laaja lähtöjoukko ja vastaava arvojoukko reaalimuuttujan x reaaliarvoiselle funktiolle
f(x) = 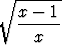 .
.
Tehtävä 26
Määritellään funktio f :

 asettamalla f(x) = |(x + 1)(x - 3)|. Laske
välin [1, 4] kuva ja välin [1, 4] alkukuva.
asettamalla f(x) = |(x + 1)(x - 3)|. Laske
välin [1, 4] kuva ja välin [1, 4] alkukuva.
Tehtävä 27
Funktio f :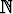

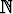 määritellään ehdoilla
määritellään ehdoilla

Millainen funktio on kyseessä?
Tehtävä 28
Miten reaalimuuttujan x funktion
f(x) = 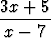
(mahdollisimman laajat) lähtö- ja maalijoukko on valittava, jotta funktio olisi bijektio? Määritä käänteisfunktion lauseke. Piirrä sekä funktion että sen käänteisfunktion kuvaaja samaan koordinaatistoon.
Tehtävä 29
Reaalimuuttujan reaaliarvoinen funktio f määritellään lausekkeella f(x) = (1 - x3)/(x2 - 1). Määritä funktiolle mahdollisimman laaja lähtöjoukko ja tätä vastaava arvojoukko. Piirrä funktion kuvaaja. Rajoita lähtöjoukkoa siten, että funktiolle saadaan käänteisfunktio. Mikä on vastaava arvojoukko? Määritä käänteisfunktion lauseke ja piirrä kuvaaja.Tehtävä 30
Muodosta reaalimuuttujan reaaliarvoisista funktioista f(x) = sin x, g(x) = x2 + 1 ja h(x) = 1 - x2 yhdistetyt kuvaukset hogof, gohof ja hofog.Tehtävä 31
Olkoot f(x) = x - 2, g(x) = 2x + 3 ja h(x) = x2 + x. Muodosta yhdistetyt funktiot fo go h ja hogof.Tehtävä 32
Olkoot f :

 ja g :
ja g : 

 reaalimuuttujan reaaliarvoisia funktioita,
f(x) =
reaalimuuttujan reaaliarvoisia funktioita,
f(x) = 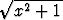 , g(x) = x2 + 1. Muodosta yhdistetyt funktiot fof, fog, gof, gog.
, g(x) = x2 + 1. Muodosta yhdistetyt funktiot fof, fog, gof, gog.
1.5 Luonnolliset luvut
Tehtävä 33
Olkoon A = {1, 2, 3}. Tutki, mitkä Peanon aksioomat A toteuttaa, kun seuraajafunktio s määritellään seuraavasti: a) s(1) = 2, s(2) = 3; b) s(1) = 2, s(2) = 3, s(3) = 1; c) s(1) = 2, s(2) = 3, s(3) = 2.Tehtävä 34
Mitkä Peanon aksioomat tyhjä joukko toteuttaa?Tehtävä 35
Todista induktiolla| a) | 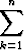 k3 = k3 = 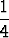 n2(n + 1)2, n n2(n + 1)2, n  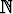 , , | ||
| b) | 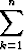 k22k = (n2 - 2n + 3) 2n+1 - 6, n k22k = (n2 - 2n + 3) 2n+1 - 6, n  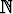 , , | ||
| c) | 1 . 3 + 3 . 5 + . . . + (2n - 1)(2n + 1) = 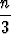 (4n2 + 6n - 1), n (4n2 + 6n - 1), n  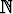 , , | ||
| d) | 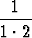 + + 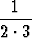 + . . . + + . . . + 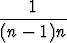 = = 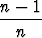 , n = 2, 3, . . . , , n = 2, 3, . . . , | ||
| e) | (1 + 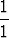 )1(1 + )1(1 + 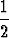 )2. . . (1 + )2. . . (1 + 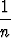 )n = )n = 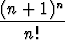 , n , n  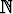 . . |
Tehtävä 36
Luvut xn, n
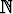 , määritellään siten, että x1 = 1 ja xn+1 = xn + 2
, määritellään siten, että x1 = 1 ja xn+1 = xn + 2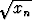 + 1,
n = 1, 2, 3, . . . . Osoita induktiota käyttäen, että kaikki luvut xn ovat kokonaislukuja.
+ 1,
n = 1, 2, 3, . . . . Osoita induktiota käyttäen, että kaikki luvut xn ovat kokonaislukuja.
Tehtävä 37
Olkoon x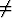 ± 1. Todista induktiolla
± 1. Todista induktiolla
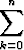
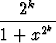 =
= 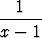 +
+ 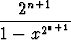 , n = 0, 1, 2, . . . .
, n = 0, 1, 2, . . . .
Tehtävä 38
Laske seuraavat summat ja tulot:
a)  k 2k, b)
k 2k, b) 
 jk, c)
jk, c) 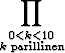 3k.
3k.
Tehtävä 39
Tutki, montako aijk-termiä on kolminkertaisessa summassa

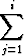
 aijk
aijk
ja laske summa, kun aijk = ijk.
1.6 Lukumäärän laskemisesta
Tehtävä 40
Muodosta joukkojen a) {a, b}, b) {a, b, c} kaikki osajoukot. Montako näitä on?Tehtävä 41
Montako erilaista viiden kortin sarjaa voidaan korttipakasta vetää, kun a) kiinnitetään, b) ei kiinnitetä huomiota korttien järjestykseen?Tehtävä 42
Neljä punaista, kolme vihreää ja kaksi sinistä palloa asetetaan jonoon. Kuinka monta erinäköistä jonoa saadaan, kun samanväriset pallot ovat keskenään identtisiä?Tehtävä 43
Kuinka monta erilaista henkilötunnusta on (Suomessa) periaatteessa olemassa? Tunnuksen muoto on ppkkvv-nnnr, missä on aluksi syntymäpäivä (ppkkvv), sitten juokseva numero (nnn) ja lopuksi tarkistusmerkki (r). Tarkistusmerkki määräytyy jakolaskun ppkkvvnnn/31 jakojäännöksestä. Rajoitutaan tarkastelemaan sadan vuoden jaksoa ja oletetaan, että karkausvuosia tähän jaksoon mahtuu 25.Tehtävä 44
Olkoon joukon A alkioiden lukumäärä #A = m < . Kuinka monta erilaista
p (p < m) alkion osajoukkoa joukon A alkioista voidaan muodostaa? Entä osajonoa?
(Joukon alkiot ovat aina keskenään eri suuria, ts. jokainen alkio mainitaan vain kerran;
jonossa sama alkio voi esiintyä useita kertoja.)
. Kuinka monta erilaista
p (p < m) alkion osajoukkoa joukon A alkioista voidaan muodostaa? Entä osajonoa?
(Joukon alkiot ovat aina keskenään eri suuria, ts. jokainen alkio mainitaan vain kerran;
jonossa sama alkio voi esiintyä useita kertoja.)
Tehtävä 45
Olkoon joukon A alkioiden lukumäärä #A = m < ja joukon B alkioiden
lukumäärä #B = n <
ja joukon B alkioiden
lukumäärä #B = n <  . Osoita, että erilaisia funktioita A
. Osoita, että erilaisia funktioita A  B on nm kappaletta.
B on nm kappaletta.
Tehtävä 46
Olkoot A ja B äärellisiä joukkoja, #A = m, #B = n. Olkoon S(m, n) surjektioiden A B lukumäärä. Osoita, että tälle pätee
B lukumäärä. Osoita, että tälle pätee
| S(m, 1) | = 1, | ||
| S(m, n) | = nm -  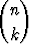 S(m, k), n = 2, 3, . . . . S(m, k), n = 2, 3, . . . . |
Tehtävä 47
Laske edellisessä tehtävässä esitettyjen kaavojen avulla surjektioiden määrä S(m, n), kun 1 < m < 4, 1 < n < 4. Mieti, voidaanko tulos saada jollakin muulla tavalla, kun a) m = n, b) m < n.Tehtävä 48
Teekkari saattoi 1970-luvun puolivälissä suorittaa jopa kuusi matematiikan kurssia — kutsuttakoon näitä seuraavassa nimillä A, B, C, D, E, F — joissa oli yhteisiä osia. Kullakin kurssilla oli suorituspistearvonsa (vastaa nykyisiä opintoviikkoja) ja kurssien yhteislaajuuden selvittämiseksi määriteltiin myös kurssien kaksittaisille, kolmittaisille jne. leikkauksille suorituspistearvot. Nämä olivat seuraavat:A: 3.5, B: 2, C: 3, D: 3.5, E: 7.5, F: 5.5,
A
 C: 1.5, A
C: 1.5, A D: 1, B
D: 1, B D: 0.5, C
D: 0.5, C D: 1,
D: 1,
A
 C
C D: 1.
D: 1.
Muiden kombinaatioiden leikkaukset olivat tyhjiä. Montako suorituspistettä sai teekkari, joka oli suorittanut kaikki kuusi kurssia?
Tehtävä 49
Laitumella on lauma nautakarjaa. Laumassa on 83 täysin ruskeata eläintä, 77 sarvipäätä, 36 sukupuoleltaan sonnia, 22 ruskeata sarvipäätä, 15 ruskeata sonnia, 25 sarvipäistä sonnia ja 7 ruskeata sarvipäistä sonnia. Muunlaisia eläimiä ei laumassa ole. Kuinka monta eläintä laumassa on kaikkiaan?Tehtävä 50
Osoita, että rationaalilukuja on yhtä paljon kuin luonnollisia lukuja, ts. että rationaalilukujen ja luonnollisten lukujen joukot ovat yhtä mahtavia.Tehtävä 51
Osoita, että avoimella välillä ]0, 1[ on reaalilukuja yhtä paljon kuin koko reaalilukujoukossa, ts. että väli ]0, 1[ ja reaalilukujoukko ovat yhtä mahtavia.
ovat yhtä mahtavia.