2 Reaaliluvut
2.1 Aksioomat
Tehtävä 52
Määritä seuraavien joukkojen supremum, infimum, maksimi ja minimi, mikäli nämä ovat olemassa:a) { x   | (x + 1)(x - 2)(x + 4) > 0 }, | (x + 1)(x - 2)(x + 4) > 0 }, | |||
b) { x   | |x| + |x + 2| < 5 }, c) { x | |x| + |x + 2| < 5 }, c) { x   | |x||x + 2| < 5 }, | |x||x + 2| < 5 }, | |||
d) { 2 - 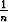 | n | n  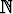 }, e) { }, e) {  | n | n  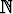 }, f) { }, f) { 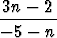 | n | n  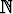 }. }. |
Tehtävä 53
Piirrä reaalimuuttujan reaaliarvoisen funktion a) f(x) = |x| + |x + 2|, b) f(x) = |x||x + 2| kuvaaja. Päättele tästä joukon a) { x
 | |x| + |x + 2| < 5 },
b) { x
| |x| + |x + 2| < 5 },
b) { x 
 | |x||x + 2| < 5 } supremum ja infimum.
| |x||x + 2| < 5 } supremum ja infimum.
Tehtävä 54
Olkoot A ja B kaksi ei-tyhjää reaalilukujoukkoa, joiden alkioille pätee a < b kaikilla a A, b
A, b  B. Todista, että sup A < inf B.
B. Todista, että sup A < inf B.
Tehtävä 55
Olkoon S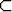
 ylhäältä rajoitettu joukko, G = sup S ja
ylhäältä rajoitettu joukko, G = sup S ja  > 0. Todista, että on
olemassa x
> 0. Todista, että on
olemassa x  S, jolle pätee x > G -
S, jolle pätee x > G -  .
.
Tehtävä 56
Olkoon S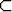
 ei-tyhjä rajoitettu joukko. Todista: Jos inf S = sup S, niin
joukossa S on täsmälleen yksi alkio.
ei-tyhjä rajoitettu joukko. Todista: Jos inf S = sup S, niin
joukossa S on täsmälleen yksi alkio.
Tehtävä 57
Olkoon S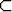
 rajoitettu joukko ja T = { x
rajoitettu joukko ja T = { x 
 | -x
| -x  S }. Osoita, että
infT = - sup S.
S }. Osoita, että
infT = - sup S.
Tehtävä 58
Todista reaalilukujen aksioomiin perustuen Arkhimedeen lause (aksiooma): Jos a ja b ovat kaksi positiivista reaalilukua, niin on olemassa luonnollinen luku n siten, että na > b.Tehtävä 59
Todista reaalilukujen aksioomien pohjalta: Jos x > 0 ja y < 0, niin xy < 0.2.2 Reaalilukujen osajoukot
Tehtävä 60
Olkoot a ja b kaksi reaalilukua, a < b. Todista, että on olemassa rationaaliluku r, jolle pätee a < r < b.Tehtävä 61
Olkoot a ja b kaksi reaalilukua, a < b. Todista, että on olemassa irrationaaliluku r, jolle pätee a < r < b.Tehtävä 62
Todista, että jos x on irrationaalikuku, niin myös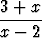 on irrationaalinen.
on irrationaalinen.
Tehtävä 63
Todista, että ei voi olla rationaaliluku.
ei voi olla rationaaliluku.
2.3 Yhtälöitä ja epäyhtälöitä
Tehtävä 64
Osoita: a) max{a, b} = (a + b + |a - b|), b) min{a, b} =
(a + b + |a - b|), b) min{a, b} =  (a + b - |a - b|).
(a + b - |a - b|).
Tehtävä 65
Ratkaise epäyhtälöt a) 4x2 - 13x + 4 < 1, b) > 1 + x, c) 2x3 > x2 + 1,
d) 5x - 4 < x2 < 25.
> 1 + x, c) 2x3 > x2 + 1,
d) 5x - 4 < x2 < 25.
Tehtävä 66
Ratkaise epäyhtälöt a) 2|x - 2| < x + 2, b) |1 - |x|| > 2, c) |7x + 21| + 9 < x2.Tehtävä 67
Olkoon x
 . Todista:
. Todista:
|x| < 

 < 1.
< 1.
Tehtävä 68
Osoita algebraa käyttäen: a < b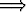 a3 < b3.
a3 < b3.
Tehtävä 69
Olkoot a ja b positiivisia. Osoita: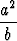 +
+  > a + b.
> a + b.
Tehtävä 70
Osoita algebraa käyttäen: a > 0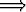 a +
a +  > 2.
> 2.
Tehtävä 71
Todista kaava
 (-1)k
(-1)k = 0, n
= 0, n 
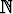 .
.
Tehtävä 72
Laske binomikertoimien summa
 .
.
Tehtävä 73
Näytä oikeaksi kaava
 + 2
+ 2 +
+  =
=  ,
,
missä on oletettava n > 4, 2 < k < n - 2. Mikä on kaavan tulkinta Pascalin kolmion avulla?
Tehtävä 74
Laske summien a + b + c, a + b + c + d ja a + b + c + d + e potensseja, ja tutki, millaisia kertoimia lausekkeissa esiintyy. Miten binomikertoimet mahtavat yleistyä multinomikertoimiksi?Tehtävä 75
Teekkari Sini Silmäinen on opintojensa alussa tehnyt Luotto-Tappio-Pankin kanssa lainasopimuksen, jonka mukaan hän nostaa jokaisen opiskeluvuoden alussa opintolainaa 20 000 mk. Vuotuinen lainakorko on 15 %, mutta opiskeluaikana ei korkoa tarvitse maksaa, vaan kertynyt korko liitetään jokaisen vuoden lopussa lainapääomaan. Paljonko teekkarilla on velkaa, kun hän 12 vuoden opintojen jälkeen lopulta valmistuu?2.4 Liukuluvut
Tehtävä 76
Oktaalijärjestelmän kantaluku on 8 ja sen numeroita merkitään 0, 1, 2, 3, 4, 5, 6, 7. Lausu kymmenjärjestelmän luvut a) 1000, b) 5432, c) 0.1 ja d) 5432.1 oktaalijärjestelmässä.Tehtävä 77
Heksadesimaalijärjestelmän kantaluku on 16 ja sen numerot ovat 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F. Lausu luvut 123, ABC ja 1A2B a) kymmenjärjestelmässä, b) oktaalijärjestelmässä, c) binäärijärjestelmässä.Tehtävä 78
Kirjoita luku 10.128 liukulukuna a) kymmenjärjestelmässä, kun mantissan pituus on 4, b) binäärijärjestelmässä, kun mantissan pituus on 8.Tehtävä 79
Liukulukujärjestelmän kantalukuna on 10 ja mantissan pituutena 3. Laske tulot (234 . 582) . 379 ja 234 . (582 . 379).Tehtävä 80
Ratkaise yhtälöpari

käyttäen kymmenjärjestelmän liukulukuja, joilla mantissan pituus on 2. Riippuuko tulos laskujärjestyksestä?