3 Kompleksiluvut
3.1 Kompleksitaso
Tehtävä 81
Todista kompleksilukujen yhteen- ja kertolaskun (lukuparien avulla annettuihin) määritelmiin perustuen osittelulaki: z1(z2 + z3) = z1z2 + z1z3.Tehtävä 82
Todista kompleksilukujen yhteen- ja kertolaskun (lukuparien avulla annettuihin) määritelmiin perustuen ns. tulon nollasääntö: z1z2 = 0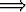 z1 = 0
z1 = 0 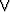 z2 = 0.
z2 = 0.
Tehtävä 83
Saata kompleksiluvut
a) (1 + i)(1 - i)5, b) 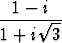
muotoon x + iy. Laske lukujen moduuli ja argumentti.
Tehtävä 84
Olkoon u = cos 0.5 + i sin 0.5 ja z0 = 1 + i. Laske kompleksiluvut wk = ukz0, k = 1, 2, 3, . . . , ja piirrä pisteiden sijainti kompleksitasossa. Miten pisteet muuttuvat, jos valitaan u = 0.9(cos 0.5 + i sin 0.5)? Millainen vaikutus luvun u potensseilla kertomisella on?Tehtävä 85
Todista, että kaikilla z1, z2
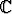 pätee
pätee
(1 + |z1|2)(1 + |z2|2) > |1 + z1z2|2.
Tehtävä 86
Olkoon Re z = Im z = a. Millä arvoilla a pätee |z - i| < |z - 3|? Piirrä kuvio.Tehtävä 87
Tutki, mitkä kompleksitason pisteet toteuttavat seuraavat ehdot:| a) |z - 1| + |z + i| = 4, b) |z + 1| - |z - i| = 1, c) |z + i| = 2|z - i|, | |||
d) arg 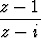 = = 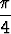 , e) arg , e) arg 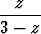 = = 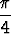 . . |
Piirrä kuviot.
Tehtävä 88
Piirrä se kompleksitason alue, jossa
a) 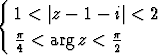 , b)
, b) 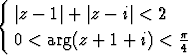 .
.
Tehtävä 89
Määritä sup{ arg z | |z - 3 - 4i| < 3, arg z [0, 2
[0, 2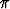 [ }. Onko kyseessä myös
maksimi?
[ }. Onko kyseessä myös
maksimi?
Tehtävä 90
Etsi kahden desimaalin tarkkuudella sup S ja inf S, kunS = { arg z | |z + 5i - 2| < 3 }.
Tässä arg z valitaan väliltä [0, 2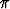 [. Piirrä kuvio.
[. Piirrä kuvio.
Tehtävä 91
Minkä käyrän piirtää a) z2, kun z piirtää käyrän arg(z - i) =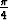 ;
b) z
;
b) z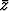 + 2z +
+ 2z + 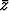 + 1, kun z piirtää ympyrän |z| = 1; c)
+ 1, kun z piirtää ympyrän |z| = 1; c) 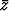 + 1 + i, kun z piirtää käyrän
|z + i| = 1? Piirrä kuviot.
+ 1 + i, kun z piirtää käyrän
|z + i| = 1? Piirrä kuviot.
Tehtävä 92
Millä kompleksitason käyrällä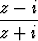 on puhtaasti imaginaarinen?
on puhtaasti imaginaarinen?
3.2 Kompleksilukujen potenssit ja juuret
Tehtävä 93
Laske seuraavien kompleksilukujen moduuli ja argumentti saattamatta lukuja muotoon x + iy:
a) (1 + i)6, b) (1 - i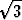 )(1 - i)2, c)
)(1 - i)2, c) 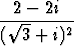 .
.
Tehtävä 94
Kehitä de Moivren kaavan avulla a) sin 5 polynomiksi, jonka muuttujana on
sin
polynomiksi, jonka muuttujana on
sin , b) tan 3
, b) tan 3 rationaalilausekkeeksi muuttujasta tan
rationaalilausekkeeksi muuttujasta tan  .
.
Tehtävä 95
Lausu a) cos 4 funktioiden cos 2
funktioiden cos 2 ja cos 4
ja cos 4 avulla, b) sin 5
avulla, b) sin 5 funktioiden sin
funktioiden sin  ,
sin3
,
sin3 ja sin 5
ja sin 5 avulla.
avulla.
Tehtävä 96
Laske (cos t + i sin t)5 a) de Moivren kaavan avulla, b) binomikaavan avulla. Minkälaiset trigonometrian kaavat tästä saadaan?Tehtävä 97
Laske geometrinen summa
 (cos t + i sin t)k.
(cos t + i sin t)k.
Millaiset trigonometrisia funktioita koskevat kaavat saadaan tuloksen reaali- ja imaginaariosasta? Piirrä summafunktion reaaliosan ja imaginaariosan kuvaajat tapauksissa n = 5, 25, 100.
Tehtävä 98
Määritä seuraavien juurien kaikki arvot:
a) 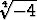 , b)
, b) 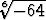 , c)
, c) 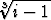 , d)
, d)  , e)
, e) 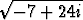 .
.
Tehtävä 99
Määritä viiden desimaalin tarkkuudella kaikki ne kompleksiluvut, joiden viides potenssi = 1. Piirrä kuvio lukujen sijainnista kompleksitasossa.Tehtävä 100
Juuren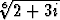 likiarvo on 1.2217 + 0.2019i. Piirrä kuva, jossa
juuren kaikki arvot on sijoitettu kompleksitasoon (laskematta juurten likiarvoja).
likiarvo on 1.2217 + 0.2019i. Piirrä kuva, jossa
juuren kaikki arvot on sijoitettu kompleksitasoon (laskematta juurten likiarvoja).
Tehtävä 101
Olkoon z =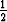 (1 + i
(1 + i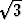 ). Tutki, millä kokonaisluvuilla n pätee zn = z.
). Tutki, millä kokonaisluvuilla n pätee zn = z.
Tehtävä 102
Olkoon = cos
= cos 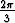 +i sin
+i sin 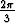 . Laske a) (a
. Laske a) (a +b
+b 2)(a
2)(a 2+b
2+b ), b) (a+b+c)(a+b
), b) (a+b+c)(a+b +c
+c 2)(a+b
2)(a+b 2+c
2+c ).
).
Tehtävä 103
Olkoon f(t) = cos t + i sin t reaalimuuttujan t kompleksiarvoinen funktio ja g(z) = Im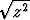 kompleksimuuttujan z reaaliarvoinen funktio. Piirrä reaalimuuttujan
reaaliarvoisen funktion gof kuvaaja. Valitse riittävän pitkä tarkasteluväli. Vertaa
kuvaajaa tapaukseen g(z) = Im z. Miksi kuvaaja näyttää sellaiselta kuin näyttää?
kompleksimuuttujan z reaaliarvoinen funktio. Piirrä reaalimuuttujan
reaaliarvoisen funktion gof kuvaaja. Valitse riittävän pitkä tarkasteluväli. Vertaa
kuvaajaa tapaukseen g(z) = Im z. Miksi kuvaaja näyttää sellaiselta kuin näyttää?
Tehtävä 104
Laske numeerisesti jollakin tietokoneohjelmalla (-1) . Yritä selittää saamasi
tulos. Mikä mahtaa olla tarkka arvo?
. Yritä selittää saamasi
tulos. Mikä mahtaa olla tarkka arvo?
Tehtävä 105
Laske numeerisesti jollakin tietokoneohjelmalla ii. Yritä selittää saamasi tulos.3.3 Polynomeista
Tehtävä 106
Ratkaise seuraavat yhtälöt käyttäen toisen asteen yhtälön ratkaisukaavoja; saata juuret muotoon x + iy.| a) z2 + 2iz - i - 1 = 0, b) z2 - 4iz - 4 + i = 0, c) z2 - (3 + 5i)z + (-4 + 7i) = 0, | |||
d) z4 - 2z2 + 4 = 0, e) z4 + (1 - 2i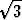 )z2 - 3 - i )z2 - 3 - i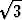 = 0. = 0. |
Tehtävä 107
Määritä

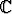 siten, että z = 1 + i on yhtälön
siten, että z = 1 + i on yhtälön 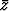 3 =
3 =  + i juuri. Esitä muut
juuret napakoordinaattimuodossa.
+ i juuri. Esitä muut
juuret napakoordinaattimuodossa.