4 Matriisit ja vektorit
4.1 Matriisin käsite
4.2 Matriisialgebra
Tehtävä 110
Olkoon
A =  , B =
, B =  .
.
Laske A + B,  A +
A +  B, AB ja BA.
B, AB ja BA.
Tehtävä 111
Olkoon A = ja B =
ja B =  T. Laske AB ja
BA.
T. Laske AB ja
BA.
Tehtävä 112
Olkoon
A = 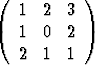 , x =
, x = 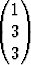 .
.
Minkä kokoisia matriiseja ovat xTx, xxT, Ax, xTAx ja xxTA? Laske ne.
Tehtävä 113
Olkoon matriisi, jonka kaikki alkiot ovat = 1, ja olkoon
matriisi, jonka kaikki alkiot ovat = 1, ja olkoon  lävistäjämatriisi, jonka lävistäjäalkiot ovat 1, 2 ja 3. Laske A
lävistäjämatriisi, jonka lävistäjäalkiot ovat 1, 2 ja 3. Laske A ja
ja  A.
A.
Tehtävä 114
Olkoon
A = 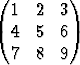 , u =
, u =  ;
;
laske uT Au, uTu, uuT.
Tehtävä 115
Olkoon
A =  .
.
Laske potenssit Ak, k = 1, 2, 3, . . . , 1992.
Tehtävä 116
Millä tyyppiä koskevilla oletuksilla matriisit AB ja BA ovat a) molemmat määriteltyjä, b) samaa tyyppiä?Tehtävä 117
Onko matriiseille voimassa a) (A + B)2 = A2 + B2 + 2AB, b) (A + B)(A - B) = A2 - B2?Tehtävä 118
Todista matriisialgebran osittelulaki A(B + C) = AB + AC.Tehtävä 119
Olkoon A neliömatriisi ja olkoot B ja C samantyyppisiä matriiseja. Todista: Jos A on säännöllinen, niin AB = AC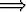 B = C.
B = C.
Tehtävä 120
Todennäköisyyslaskennassa tarkastellaan ns. Markovin prosesseja, jotka kuvaavat systeemiä, joka voi olla äärellisen monessa eri tilassa. Siirtymistodennäköisyydet tilasta toiseen muodostavat neliömatriisin A, jonka kaikki alkiot ovat > 0 ja jossa vaakariveittäin lasketut summat ovat = 1. Muodosta tällaisia matriiseja ja tutki matriisin An alkioiden raja-arvoja, kun n
 . Esitä hypoteesi alkioiden käyttäytymisestä.
. Esitä hypoteesi alkioiden käyttäytymisestä.
Tehtävä 121
Matriisin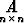 alkiot ovat
alkiot ovat  ij = ij. Kirjoita matriisi A ja laske matriisitulo
AAT tapauksessa n = 3. Laske yleisessä tapauksessa (arvolla n) tulomatriisin AAT
kohdassa (i, j) oleva alkio indeksien i ja j funktiona.
ij = ij. Kirjoita matriisi A ja laske matriisitulo
AAT tapauksessa n = 3. Laske yleisessä tapauksessa (arvolla n) tulomatriisin AAT
kohdassa (i, j) oleva alkio indeksien i ja j funktiona.
Tehtävä 122
Olkoot A ja B kokoa 10 × 10 olevia matriiseja, joiden alkiot ovat ij = i + j,
ij = i + j,  ij = i - j. Laske tulomatriisin C = AB alkio
ij = i - j. Laske tulomatriisin C = AB alkio 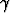 ij indeksien i, j
funktiona.
ij indeksien i, j
funktiona.
Tehtävä 123
Laske (AB)k, k
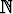 , kun
, kun
A =  , B =
, B = 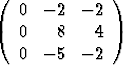 .
.
Tehtävä 124
Muodosta jokin pystyvektori x. Laske r = xTx ja u = x/ . Mitä r kertoo
vektorin x alkioista? Mikä ominaisuus on vektorin u alkioilla? Muodosta matriisi
H = I - 2uuT ja sen käänteismatriisi H-1. Miten nämä suhtautuvat toisiinsa? Onko H
symmetrinen tai ortogonaalinen?
. Mitä r kertoo
vektorin x alkioista? Mikä ominaisuus on vektorin u alkioilla? Muodosta matriisi
H = I - 2uuT ja sen käänteismatriisi H-1. Miten nämä suhtautuvat toisiinsa? Onko H
symmetrinen tai ortogonaalinen?
Tehtävä 125
Osoita, että edellisen tehtävän matriisi H on involutorinen, ts. HH = I riippumatta vektorista x. Mitä tämä tulos sanoo käänteismatriisista?Tehtävä 126
Hae kaikki matriisit B, jotka kommutoivat matriisin
A = 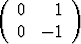
kanssa, ts. joille pätee AB = BA.
Tehtävä 127
Osoita, että jos A ja B ortogonaalimatriiseja, niin myös AB ja A-1 ovat ortogonaalisia.Tehtävä 128
Olkoon A kokoa 3 × 3 oleva ortogonaalimatriisi, jonka alkioista tiedetään seuraavaa:
 11 =
11 =  ,
,  12 = -
12 = - ,
,  13 > 0,
13 > 0,  21 < 0,
21 < 0,  22 =
22 =  .
.
Määritä A ja A-1.
Tehtävä 129
Todista, että jos matriisille A pätee AT + A = O ja käänteismatriisi (I + A)-1 on olemassa, niin matriisi B = (I + A)-1(I - A) on ortogonaalinen.Tehtävä 130
Todista, että jokainen ortogonaalinen 2 × 2-matriisi voidaan kirjoittaa jompaankumpaan seuraavista muodoista:
 tai
tai 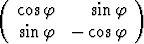 .
.
4.3 Lineaarinen yhtälöryhmä
Tehtävä 131
Totea, että yhtälöryhmän
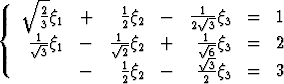
kerroinmatriisi on ortogonaalinen ja käytä tätä tietoa hyväksi yhtälöryhmän ratkaisemisessa.
Tehtävä 132
Olkoon| a) | A =  , , | C = 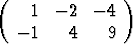 , , | b =  , , | ||||||||||||
| b) | A =  , , | C =  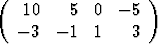 , , | b = 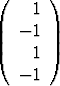 . . |
Laske tulo CA. Tutki, voidaanko lineaarinen yhtälöryhmä Ax = b ratkaista kertomalla se vasemmalta matriisilla C. Mitä tällöin saadaan ratkaisuvektoriksi x? Onko kyseessä matriisiyhtälön ratkaisu?
Tehtävä 133
Ratkaise Gaussin algoritmilla lineaariset yhtälöryhmät| a) |  , , | b) |  , , | ||||
| c) | 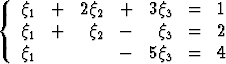 , , | d) | 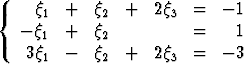 . . |
Tehtävä 134
Ratkaise Gaussin algoritmilla yhtälöryhmä Ax = b, kun| a) | A =  , , | b =  , , | b) | A = 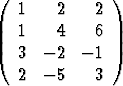 , , | b =  , , | ||||||||||||||||||
| c) | A =  , , | b =  , , | d) | A = 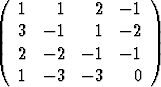 , , | b =  . . |
Tehtävä 135
Olkoon
A =  , b =
, b =  .
.
Tutki yhtälöryhmän Ax = b ratkaisujen lukumäärää lukujen  ,
,  eri arvoilla.
eri arvoilla.
Tehtävä 136
Ratkaise yhtälöryhmä Ax = b, kun
A = 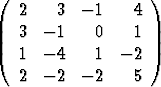 , b =
, b =  .
.
Tehtävä 137
Olkoon
A =  , b =
, b = 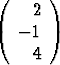 .
.
Osoita, että yhtälöryhmällä Ax = b ei ole ratkaisua. Tietyssä mielessä (pienimmän
neliösumman mielessä) mahdollisimman hyvä ratkaisu (joka ei kuitenkaan — tietenkään
— toteuta yhtälöryhmää) saadaan ratkaisemalla matriisiyhtälö ATAx = ATb.
Muodosta tämä yhtälöryhmä ja ratkaise se. Piirrä ryhmän yhtälöiden kuvaajat
sekä saatu pienimmän neliösumman periaatteen mukainen ratkaisu tasoon  2.
2.
4.4 Vektoriavaruus  n
n
Tehtävä 138
Tutki avaruuden 4 vektoreiden
4 vektoreiden 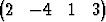 T,
T,  T,
T,
 T lineaarista riippumattomuutta.
T lineaarista riippumattomuutta.
Tehtävä 139
Tutki, ovatko vektorit T,
T,  T,
T,  T
lineaarisesti riippumattomia. Voidaanko vektori
T
lineaarisesti riippumattomia. Voidaanko vektori  T lausua näiden
lineaariyhdistelynä? Jos voidaan, niin onko esitys yksikäsitteinen?
T lausua näiden
lineaariyhdistelynä? Jos voidaan, niin onko esitys yksikäsitteinen?
Tehtävä 140
Osoita, että vektorit T,
T,  T ja
T ja 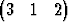 T muodostavat
avaruuden
T muodostavat
avaruuden  3 kannan. Laske vektorin
3 kannan. Laske vektorin  T koordinaatit tässä kannassa.
T koordinaatit tässä kannassa.
Tehtävä 141
Osoita, että vektorit a1 = T, a2 =
T, a2 =  T, a3 =
T, a3 = 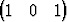 T
muodostavat avaruuden
T
muodostavat avaruuden  3 kannan. Mitkä ovat vektorin x =
3 kannan. Mitkä ovat vektorin x =  T koordinaatit
tässä kannassa?
T koordinaatit
tässä kannassa?
Tehtävä 142
Tutki, muodostavatko vektorit
a1 =  T, a2 =
T, a2 =  T, a3 =
T, a3 =  T, a4 =
T, a4 = 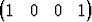 T
T
avaruuden  4 kannan. Voidaanko vektori x =
4 kannan. Voidaanko vektori x =  T lausua näiden
lineaariyhdistelynä?
T lausua näiden
lineaariyhdistelynä?
Tehtävä 143
Millä lukuja ,
,  ,
, 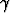 ,
, 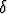 koskevalla ehdolla vektorit
koskevalla ehdolla vektorit  x +
x +  y ja
y ja 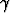 x +
x + 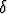 y ovat
lineaarisesti riippumattomia, jos vektorit x ja y a) ovat, b) eivät ole lineaarisesti
riippumattomia?
y ovat
lineaarisesti riippumattomia, jos vektorit x ja y a) ovat, b) eivät ole lineaarisesti
riippumattomia?
Tehtävä 144
Todista, että jos vektorit a1, . . . , ap ovat lineaarisesti riippuvia, niin myös vektorit 1 a1 , . . . ,
1 a1 , . . . ,  pap ovat. Todista, että jos a1, . . . , ap ovat lineaarisesti
riippumattomia, niin vektorit
pap ovat. Todista, että jos a1, . . . , ap ovat lineaarisesti
riippumattomia, niin vektorit  1a1, . . . ,
1a1, . . . ,  pap ovat lineaarisesti riippumattomia, jos ja
vain jos tulo
pap ovat lineaarisesti riippumattomia, jos ja
vain jos tulo  1. . .
1. . .  p on
p on  0.
0.
Tehtävä 145
Olkoot vektorit a1, . . . , ap lineaarisesti riippumattomia. Tutki, ovatko seuraavat vektorisysteemit lineaarisesti riippumattomia:| a) | a1, a2 + a1, a3 + a2, . . . , ap + ap-1, | ||
| b) | a1 - ap, a2 - a1, a3 - a2, . . . , ap - ap-1, | ||
| c) | a1, . . . , aj-1, aj +  ak, aj+1, . . . , ap, missä k ak, aj+1, . . . , ap, missä k j. j. |
4.5 Determinantti
Tehtävä 146
Laske Gaussin algoritmilla, alideterminanttikehitelmää käyttäen ja Sarrus’n säännöllä seuraavat determinantit:
a) 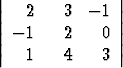 , b)
, b) 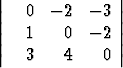 , c)
, c)  .
.
Tarkista tulokset jollakin tietokoneohjelmalla.
Tehtävä 147
Laske sekä Gaussin algoritmilla että alideterminanttikehitelmää käyttäen seuraavat determinantit:
a)  , b)
, b)  , c)
, c)  .
.
Tarkista tulokset jollakin tietokoneohjelmalla.
Tehtävä 148
Laske determinantti
 .
.
Tehtävä 149
Laske seuraavat determinantit sopivia determinantin laskusääntöjä käyttäen:
a)  , b)
, b) 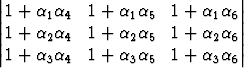 .
.
Tehtävä 150
Millä lukuja ja
ja  koskevilla ehdoilla seuraavat determinantit ovat
= 0?
koskevilla ehdoilla seuraavat determinantit ovat
= 0?
a) 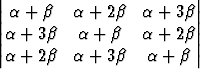 , b)
, b)  .
.
Tehtävä 151
Olkoon
A =  .
.
Laske det ((-5AAT)7) käyttämällä determinantin laskusääntöjä.
Tehtävä 152
Matriisista tiedetään, että se ei ole symmetrinen ja että sillä on
ominaisuus AT =
tiedetään, että se ei ole symmetrinen ja että sillä on
ominaisuus AT =  A eräällä skalaarilla
A eräällä skalaarilla  . Mitä tämän perusteella voidaan päätellä
matriisista A ja skalaarista
. Mitä tämän perusteella voidaan päätellä
matriisista A ja skalaarista  ?
?
Tehtävä 153
Tutki, millä luvun arvoilla avaruuden
arvoilla avaruuden  4 vektorit (
4 vektorit ( , 1, 1, 1), (1,
, 1, 1, 1), (1,  , 1, 1),
(1, 1,
, 1, 1),
(1, 1,  , 1), (1, 1, 1,
, 1), (1, 1, 1,  ) ovat lineaarisesti riippuvia. Millä luvun
) ovat lineaarisesti riippuvia. Millä luvun  arvoilla vektori
(1, -1, -3, 3) voidaan lausua em. vektoreiden lineaariyhdistelynä?
arvoilla vektori
(1, -1, -3, 3) voidaan lausua em. vektoreiden lineaariyhdistelynä?
Tehtävä 154
Muodosta jokin pystyvektori x, jolle pätee xTx = 1, ja tämän avulla matriisi H = I - 2xxT. Laske matriisin H determinantti. Kokeile erilaisia vektoreita x ja esitä hypoteesi determinantista.Tehtävä 155
Eräs tietokone suorittaa keskimäärin miljardi liukulukulaskutoimitusta (yhteen-, vähennys-, kerto- tai jakolaskua) sekunnissa. Kauanko koneella kestää laskea a) 10-rivinen, b) 100-rivinen determinantti 1) suoraan permutaatioihin perustuvan määritelmän avulla, 2) Gaussin algoritmilla?4.6 Käänteismatriisi
Tehtävä 156
Määritä Gaussin algoritmilla ja alideterminanttien avulla A-1, kun| a) | A =  , , | b) | A =  , , | ||||
| c) | A = 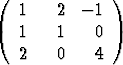 , , | d) | A = 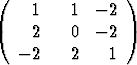 , , | ||||
| e) | A =  , , | f) | A =  . . |
Tarkista tulokset jollakin tietokoneohjelmalla.
Tehtävä 157
Laske käänteismatriisi matriisille
 .
.
Tehtävä 158
Olkoon
A = 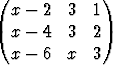 .
.
Tutki, millä muuttujan x arvoilla a) matriisilla ei ole käänteismatriisia, b) sen pystyvektorit ovat lineaarisesti riippumattomia.
Tehtävä 159
Tutki, millä ehdolla matriisin

a) pysty-, b) vaakavektorit ovat lineaarisesti riippumattomia.
Tehtävä 160
Olkoon
A =  , b =
, b = 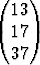 .
.
Ratkaise yhtälöryhmä Ax = b.
Tehtävä 161
Kuten edellinen tehtävä, mutta matriisin oikean alanurkan alkio onkin 9. Analysoi tilannetta muodostamalla matriisin determinantti ja määrittämällä matriisin lineaarisesti riippumattomien pystyvektoreiden lukumäärä.4.7 Lineaarikuvaus
Tehtävä 162
Lineaarikuvaus F : n
n 
 3 kuvaa avaruuden
3 kuvaa avaruuden  n vektorit x1, x2 ja
x3 vektoreille (0, 2, -1), (1, 2, 3) ja (1, -1, 0). Laske vektorin 3x1 - 2x2 + x3
kuva.
n vektorit x1, x2 ja
x3 vektoreille (0, 2, -1), (1, 2, 3) ja (1, -1, 0). Laske vektorin 3x1 - 2x2 + x3
kuva.
Tehtävä 163
Voiko kuvaus F : 3
3 
 3 olla lineaarinen, jos
3 olla lineaarinen, jos
F ((0, 1, 1)) = (1, 0, 0), F ((1, 0, 1)) = (1, 1, 0), F ((1, -1, 0)) = (1, 1, 1)?
Tehtävä 164
Lineaarikuvauksella F : 2
2 
 2 on ominaisuudet F ((1, 1)) = (3, -1) ja
F ((2, -1)) = (1, 2). Laske kuvauksen matriisi (luonnolllisten kantojen suhteen) ja määritä
tämän avulla vektorin (1, -1) kuva.
2 on ominaisuudet F ((1, 1)) = (3, -1) ja
F ((2, -1)) = (1, 2). Laske kuvauksen matriisi (luonnolllisten kantojen suhteen) ja määritä
tämän avulla vektorin (1, -1) kuva.
Tehtävä 165
Olkoot F ja G lineaarikuvauksia. Todista, että yhdistetty kuvaus F oG on myös lineaarikuvaus.Tehtävä 166
Todista, että lineaarikuvaus F on injektio, jos ja vain jos F (x) = o x = o.
x = o.