5 Geometriset avaruudet
5.1 Pisteavaruus, vektoriavaruus ja koordinaattiavaruus
Tehtävä 169
Olkoon {b1, b2} tason E2 kanta ja olkoon u = 2b1 + 3b2, v = -3b1 + 2b2, w = -b1 - 2b2. Määritä vektoreiden 2u - v + w ja u + v - w koordinaattivektorit. Piirrä kuvio vektoreista tapauksessa a) b1 = i, b2 = j, b) b1 = i, b2 = i - j.Tehtävä 170
Määritä siten, että vektori a
siten, että vektori a 
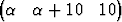 T on vektorin
b
T on vektorin
b 
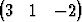 T suuntainen. Ovatko vektorit saman- vai vastakkaissuuntaiset?
T suuntainen. Ovatko vektorit saman- vai vastakkaissuuntaiset?
Tehtävä 171
Osoita, että kolmiulotteisen avaruuden E3 vektorit b1 = 2i + 7j + 5k, b2 = -i - 8j + 3k, b3 = i + j - 5k muodostavat kannan ja laske vektorin 6i + 3j + 37k koordinaatit tässä kannassa.Tehtävä 172
Olkoon {b1, b2, b3} avaruuden E3 kanta ja olkoot
u 
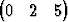 T, v
T, v 
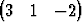 T, w
T, w 
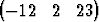 T
T
kolme tässä kannassa esitettyä vektoria. Osoita, että u, v ja w ovat saman tason suuntaisia ja lausu u vektoreiden v ja w lineaariyhdistelynä.
Tehtävä 173
Tutki, millä ehdolla seuraavat tason E2 kannassa {b1, b2} annetut vektoriparit ovat lineaarisesti riippuvia:
a) 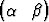 T,
T, 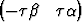 T, b)
T, b) 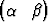 T,
T, 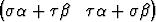 T.
T.
Tehtävä 174
Olkoon annettuna kolme vektoria eräässä avaruuden E3 kannassa:
u 
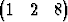 T, v
T, v 
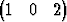 T, w
T, w 
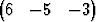 T.
T.
Määritä vektoreiden u + 7v - 2w, -u + 5v - w 7u - v + 10w koordinaattivektorit samassa kannassa. Ovatko viimeksi mainitut vektorit lineaarisesti riippumattomia?
Tehtävä 175
Tutki seuraavien vektorisysteemien lineaarista riippuvuutta, kun kantana on b1 = i + 3j + 5k, b2 = 7i + 11j + 13k, b3 = 17i + 19j + 23k:| a) | {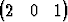 T, T, 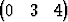 T, T, 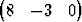 T}, T}, | ||
| b) | {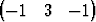 T, T, 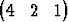 T, T, 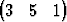 T}, T}, | ||
| c) | {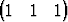 T, T, 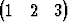 T, T, 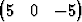 T}, T}, | ||
| d) | {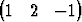 T, T, 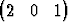 T, T, 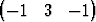 T, T, 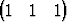 T}. T}. |
Tehtävä 176
Olkoot vektorit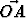 ,
, 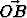 ja
ja 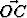 lineaarisesti riippumattomia. Todista,
että myös vektorit
lineaarisesti riippumattomia. Todista,
että myös vektorit 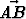 ja
ja 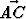 ovat (keskenään) lineaarisesti riippumattomia.
ovat (keskenään) lineaarisesti riippumattomia.
Tehtävä 177
Kolmion ABC keskiö olkoon M. Koordinaatiston origona olkoon M ja kantavektoreina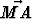 ja
ja 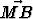 . Laske kolmion kärkipisteiden ja sivujen keskipisteiden
koordinaatit.
. Laske kolmion kärkipisteiden ja sivujen keskipisteiden
koordinaatit.
Tehtävä 178
Kolmiossa ABC piste O puolittaa sivun AB, piste E1 jakaa sivun BC suhteessa 1 : 2 ja piste E2 sivun CA suhteessa 1 : 3. Määritä kolmion kärkipisteiden koordinaatit siinä koordinaatistossa, jonka origona on piste O ja kantavektoreina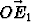 ja
ja
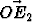 .
.
Tehtävä 179
Annettu tetraedri määrää avaruuden koordinaatiston siten, että yksi kärki on origona ja muut määrittävät kantavektoreiden loppupisteet. Määritä särmien keskipisteiden, tahkojen keskiöiden ja tetraedrin keskiön koordinaatit.Tehtävä 180
Olkoot vektorit a ja b erisuuntaisia, ts. a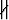 b. Määritä vektori c siten, että
a + b, b + c ja c + a muodostavat kolmion.
b. Määritä vektori c siten, että
a + b, b + c ja c + a muodostavat kolmion.
Tehtävä 181
Olkoon piste M kolmion ABC keskiö (keskijanojen leikkauspiste). Osoita, että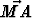 +
+ 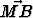 +
+ 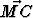 = o.
= o.
Tehtävä 182
Olkoot pisteet M ja N kolmioiden ABC ja DEF keskiöt. Osoita, että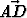 +
+ 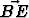 +
+ 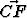 = 3
= 3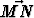 .
.
Tehtävä 183
Kolmion ABC sivut BC, CA ja AB jakautuvat pisteissä A', B' ja C' suhteessa m : n. Todista, että kolmioiden ABC ja A'B'C' keskiöt yhtyvät.Tehtävä 184
Kolmiossa ABC piste D jakaa sivun BC suhteessa p : q ja piste E sivun AB suhteessa r : s. Missä suhteessa janojen AD ja CE leikkauspiste X jakaa janan AD?Tehtävä 185
Kolmion ABC kärjestä A sivulle BC piirretty jana AD puolittaa kulman BAC. Lausu vektori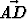 vektorien u =
vektorien u = 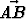 ja v =
ja v = 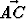 avulla, kun tiedetään, että
|
avulla, kun tiedetään, että
|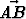 | = 3 ja |
| = 3 ja |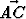 | = 2.
| = 2.
Tehtävä 186
Kolmion ABC sivuja merkitään u =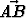 , v =
, v = 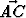 . Kärjestä A piirretyn
kulmanpuolittajan ja kärjestä C piirretyn keskijanan leikkauspiste olkoon K. Määritä |u|,
kun tiedetään, että |v| = 1 ja
. Kärjestä A piirretyn
kulmanpuolittajan ja kärjestä C piirretyn keskijanan leikkauspiste olkoon K. Määritä |u|,
kun tiedetään, että |v| = 1 ja 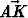 =
=  u +
u +  v.
v.
Tehtävä 187
Suunnikkaassa ABCD kärki A yhdistetään sivun DC keskipisteeseen P ja kärki B sivun AD keskipisteeseen R. Yhdysjanat leikatkoot pisteessä X. Lausu vektori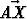 vektoreiden u =
vektoreiden u = 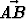 ja v =
ja v = 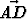 avulla.
avulla.
Tehtävä 188
Olkoot E, F , G ja H suunnikkaan ABCD sivujen AB, BC, CD ja DA keskipisteet. Piste X olkoon janojen BG ja EF leikkauspiste. Lausu vektori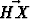 vektorien u =
vektorien u = 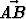 ja v =
ja v = 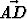 avulla.
avulla.
Tehtävä 189
Puolisuunnikkaassa ABCD, missä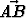
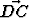 ja |
ja |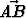 | : |
| : |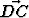 | = m > 1,
merkitään u =
| = m > 1,
merkitään u = 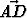 ja v =
ja v = 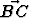 . Lausu näiden avulla vektorit
. Lausu näiden avulla vektorit 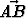 ja
ja 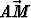 , missä M on
puolisuunnikkaan lävistäjien leikkauspiste.
, missä M on
puolisuunnikkaan lävistäjien leikkauspiste.
Tehtävä 190
Osoita vektoreita käyttäen, että tetraedrin kahden vastakkaisen särmän keskipisteiden yhdysjanoilla on yksi yhteinen piste.Tehtävä 191
Tetraedrin keskijana on kärjen ja vastakkaisen sivutahkon keskiön yhdysjana. Piste X jakakoon tetraedrin erään keskijanan kärjestä lähdettäessä suhteessa 3 : 1. Osoita, että X yhtyy edellisessä tehtävässä mainittujen yhdysjanojen leikkauspisteeseen. Miten tetraedrin neljä keskijanaa suhtautuvat toisiinsa?5.2 Käyräviivaisia koordinaatistoja
Tehtävä 192
Pisteen P suorakulmaiset avaruuskoordinaatit ovat (-2, 3, -1). Laske lieriö- ja pallokoordinaatit (tarkat arvot ja likiarvot).Tehtävä 193
Laske kolmiulotteisen avaruuden (kannassa {i, j, k} annettujen) pisteiden (1, 1, 1) ja (-1, -3, -5) pallokoordinaatit (likiarvot).Tehtävä 194
Origokeskisellä pallopinnalla sijaitseva käyrä toteuttaa pallokoordinaattiyhtälön =
= 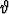 . Millainen käyrä on kysymyksessä?
. Millainen käyrä on kysymyksessä?
Tehtävä 195
Lieriön akselina on z-akseli. Lieriöpinnalla sijaitsee käyrä, jonka yhtälö lieriökoordinaateissa on z = . Millainen käyrä on kyseessä?
. Millainen käyrä on kyseessä?
5.3 Skalaaritulo
Tehtävä 196
Vektoreille a ja b pätee |a + 3b| = 16, |a - 3b| = 2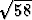 . Laske vektoreiden
sisätulo a . b.
. Laske vektoreiden
sisätulo a . b.
Tehtävä 197
Vektoreiden a ja b välinen kulma on 120o ja |a| = 3|b|. Määritä skalaari siten, että a + b ja a -
siten, että a + b ja a -  b ovat kohtisuorassa toisiaan vastaan.
b ovat kohtisuorassa toisiaan vastaan.
Tehtävä 198
Suorakulmaisessa kolmiossa ABC on suoran kulman kärjestä lähtevä korkeusjana AD. Sivujen AB ja AC pituudet ovat 5 ja 12. Laske skalaaritulot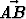 .
. 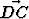 ,
,
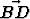 .
. 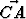 ,
, 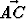 .
. 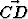 .
.
Tehtävä 199
Säännöllisen tetraedrin kärjestä lähtevät särmävektorit ovat a, b ja c. Laske vektoreiden a + b + 2c ja 2a - b välisen kulman kosini.Tehtävä 200
Avaruuden E3 kantavektoreista tiedetään seuraavaa: |b1| = |b2| = 1, |b3 | = 2, b1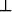 b2,
b2, 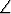 (b3, b1) =
(b3, b1) = 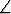 (b3, b2) = 60o. Määritä
(b3, b2) = 60o. Määritä  siten, että vektoreille
u = 2b1 +
siten, että vektoreille
u = 2b1 +  b3 ja v = b1 + 3b2 on voimassa | comp(u, v)| = | comp(v, u)|.
b3 ja v = b1 + 3b2 on voimassa | comp(u, v)| = | comp(v, u)|.
Tehtävä 201
Koordinaatiston {O, b1, b2, b3} kantavektorit muodostavat pareittain 60o kulman ja niiden pituudet ovat |b1| = 3, |b2| = 2, |b3| = 1. Muodosta vektoreiden määräämän tetraedrin pisteestä O lähtevän mediaanivektorin vektorikomponentti vektorille b1 .Tehtävä 202
Osoita skalaarituloa käyttäen, että kolmion korkeusjanat kulkevat saman pisteen kautta.Tehtävä 203
Olkoon a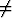 o vakiovektori ja olkoon r pisteen P paikkavektori. Millaisen
joukon muodostavat ne pisteet P , joille pätee a) (r - a) . a = 0, b) (r - a) . r = 0 ? Tarkastele
erikseen taso- ja avaruustapausta.
o vakiovektori ja olkoon r pisteen P paikkavektori. Millaisen
joukon muodostavat ne pisteet P , joille pätee a) (r - a) . a = 0, b) (r - a) . r = 0 ? Tarkastele
erikseen taso- ja avaruustapausta.
Tehtävä 204
Kolmiulotteisessa avaruudessa pisteen P ja origon yhdysjanan pituus on 5. Se muodostaa positiivisen x-akselin kanssa kulman = 32o ja positiivisen y-akselin
kanssa kulman
= 32o ja positiivisen y-akselin
kanssa kulman  = 73o. Laske pisteen P koordinaatit.
= 73o. Laske pisteen P koordinaatit.
Tehtävä 205
Olkoon a = 3i - 4j + 2k ja b = i + j - 3k. Laske kummankin vektorin skalaari- ja vektorikomponentti toisen vektorin suunnalle.Tehtävä 206
Määritä vektori, joka muodostaa yhtä suuret kulmat vektoreiden k, j + k ja i + j + k kanssa.5.4 Vektoritulo
Tehtävä 207
Määritä yksikkövektori, joka on kohtisuorassa vektoreita 2i + 3j - k ja i - j + 3k vastaan.Tehtävä 208
Muodosta ortonormeerattu oikeakätinen avaruuden E3 kanta {b1, b2, b3}, jonka vektori b1 on vektorin i + j + k suuntainen ja vektori b2 on vaakasuora, ts. xy-tason suuntainen. Määräytyykö kanta yksikäsitteisesti näistä ehdoista?Tehtävä 209
Jaa vektori u = 11i - 7j - 11k kolmeen komponenttiin, joista yksi on vektorin a = 2i - 3j + k suuntainen, toinen vektorin b = i - 2j + 4k suuntainen ja kolmas kohtisuorassa vektoreita a ja b vastaan. Miten pitkä on vektorin kohtisuora projektio tasolla, joka on vektoreiden a ja b suuntainen?Tehtävä 210
Osoita: a + b + c = o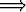 a × b = b × c = c × a.
a × b = b × c = c × a.
Tehtävä 211
Kheopsin pyramidin alkuperäinen korkeus oli 147 m ja neliönmuotoisen pohjan sivun pituus 230 m. Sijoita pyramidi sopivasti koordinaatistoon, laske pyramidin kahden vierekkäisen sivun normaalivektorit ja näiden avulla sivujen välinen (diedri)kulma.Tehtävä 212
Sijoita säännöllinen oktaedri sopivaan asentoon koordinaatistoon siten, että yksi kärki on origossa. Laske tästä kärjestä alkavien särmien vektoriesitykset ja näiden avulla tässä kärjessä kohtaavien sivutahkojen normaalivektorit. Laske näiden avulla sivutahkojen välinen diedrikulma.Tehtävä 213
Helsingistä lennetään lyhintä tietä Tokioon. Miten pitkä on matka ja mihin ilmansuuntaan Helsingistä on lähdettävä? Maapallon säde on 6370 km ja kaupunkien maantieteelliset koordinaatit seuraavat:| Helsinki: | 60o | N , | 25o | E ; | |||||||
| Tokio: | 36o | N , | 140o | E . |
(Muodosta aluksi paikkakuntien paikkavektorit maantieteellisten pallokoordinaattien avulla ja käytä sitten skalaari- ja vektorituloja.)
Tehtävä 214
Laske vektoreiden a = 2i + 3j + 4k ja b = 2i - 3j + 4k ristitulo. Laske myös vektoria a vastaava ristitulomatriisi A× ja em. ristitulo matriisitulona A×b.5.5 Vektorialgebraa
Tehtävä 215
Olkoot a, b ja x avaruuden E3 vektoreita. Johda vektorikolmitulon a × (b × x) kehityskaava muodostamalla vektoreita a ja b vastaavat ristitulomatriisit A×, B× ja laskemalla A×B×. Tulkitse A×B×x, missä x x, kehityskaavan oikeaksi puoleksi.
x, kehityskaavan oikeaksi puoleksi.
Tehtävä 216
Laske a × (b × c) sekä kahdella ristitulon muodostamisella että vektorikolmitulon kehityskaavalla, kun a = 2i + 3j - 4k, b = -3i + j + 5k, c = -2i - 2j + 3k.Tehtävä 217
Laske (a × b) × c, kun a . j = b . j = 0, c = 2i - j + 3k ja [a, b, c] = -4.Tehtävä 218
Tutki, millä ehdoilla a × (b × c) = (a × b) × c.Tehtävä 219
Olkoot a, b ja c avaruuden E3 vektoreita. Todista:[a × b, b × c, c × a] = [a, b, c]2.
Tehtävä 220
Vektorit a, b, c ovat lineaarisesti riippumattomia. Sievennä lauseke[(a × b) × (b × c)] × (c × a).
Millä ehdolla lauseke on = o?
Tehtävä 221
Osoita: |a × (a × b)|2 = |a|4|b|2 - |a|2(a . b)2.Tehtävä 222
Määritä vektorin (a × (a × (a × (a × (a × (a × b)))))) pituus, kun tiedetään, että |a| = 3, |b| = 1 ja a . b = -2.Tehtävä 223
Määritä vektori r, joka toteuttaa yhtälöparin
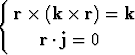 .
.
Tehtävä 224
Laske sen kolmion ala, jonka kahtena sivuna ovat vektorit i + 5j - 2k ja 3i - 2j - k.Tehtävä 225
Tetraedrin kärjet ovat (-1, -2, 4), (5, -1, 0), (2, -3, 6), (1, -1, 1). Laske tetraedrin tilavuus.Tehtävä 226
Tutki, muodostavatko a) tason E2 vektorit {2i - j, -i - j}, b) avaruuden E3 vektorit {i - j + k, 3i + 2j + k, i + j - 5k} kannan. Onko (myönteisessä tapauksessa) kanta positiivisesti vai negatiivisesti suunnistettu?Tehtävä 227
Tason E2 koordinaatistossa {O, b1, b2} on annettuna pisteet A
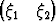 T,
B
T,
B 
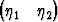 T. Osoita, että kolmion OAB pinta-ala on
T. Osoita, että kolmion OAB pinta-ala on
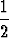 |b1||b2|| sin
|b1||b2|| sin 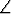 (b1, b2)|
(b1, b2)|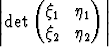 .
.
Tehtävä 228
Avaruuden E3 kolmen pisteen paikkavektorit ovat a, b ja c. Esitä menettely, jolla voidaan määrittää pisteiden kautta kulkevan ympyrän keskipisteen paikkavektori.Tehtävä 229
Kolmiulotteisen avaruuden ympyrä kulkee pisteiden (1, 2, 3), (2, -5, 3) ja (-1, 3, -6) kautta. Määritä ympyrän keskipiste, säde ja ympyrän tason normaalin suunta.5.6 Koordinaatiston vaihto
Tehtävä 230
Tason E2 kahden kannan välillä vallitsee yhteys
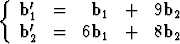 .
.
Muodosta koordinaatistonmuunnoskaavat pilkutettujen koordinaattien suhteen ratkaistuina.
Tehtävä 231
Tasossa E2 siirrytään vanhasta koordinaatistosta {O, i, j} uuteen koordinaatistoon {O', b1, b2}, missä O' 2i + j, b1 = i + j, b2 = j. Esitä
koordinaatistonmuunnos sekä uusien että vanhojen koordinaattien suhteen ratkaistuna.
2i + j, b1 = i + j, b2 = j. Esitä
koordinaatistonmuunnos sekä uusien että vanhojen koordinaattien suhteen ratkaistuna.
Tehtävä 232
Avaruuden E3 vanha kanta muodostuu vektoreistab1 = i + j + k, b2 = i + 2j + 3k, b3 = i + 4j + 9k
ja uusi kanta vektoreista
b'1 = i + 2j, b'2 = 3j + 4k, b'3 = 6i + 5k.
Origojen paikkavektorit ovat b0 = i + j ja b'0 = 2j + k. Muodosta yhtälöryhmät, joista kannanvaihtomatriisi ja origonsiirtovektori voidaan ratkaista.
Tehtävä 233
Muodosta edellisen tehtävän kannanvaihtokaavat ja muunna vanhan kannan koordinaatit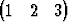 T uuteen kantaan ja takaisin.
T uuteen kantaan ja takaisin.
Tehtävä 234
Avaruuden E3 kahden kannan välillä vallitsee yhteys
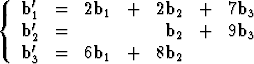 .
.
Määritä luvut  ja
ja  siten, että vektorin
siten, että vektorin  b'1 +
b'1 +  b'2 + b'3 koordinaatit kannassa
{b1 , b2 , b3 } ovat keskenään yhtä suuret.
b'2 + b'3 koordinaatit kannassa
{b1 , b2 , b3 } ovat keskenään yhtä suuret.
Tehtävä 235
Avaruuteen sijoitetaan suuntaissärmiö, jonka yhtenä kärkenä on piste P (1, 2, 3) ja jonka tästä kärjestä lähtevät särmät ovat
(1, 2, 3) ja jonka tästä kärjestä lähtevät särmät ovat
b1 = i + j + k, b2 = i + 2j + 3k, b3 = i + 4j + 9k.
Laske särmiön sivutahkojen keskipisteiden koordinaatit särmäkoordinaatistossa {P, b1 , b2 , b3 }. Muodosta koordinaatistomuunnos, jolla nämä koordinaatit saadaan lasketuiksi {O, i, j, k} -koordinaatistossa ja laske koordinaatit.
Tehtävä 236
Tason koordinaatistossa {O, b1, b2} on koordinaatiston {O', b'1, b'2} '1-akselin yhtälö 2
'1-akselin yhtälö 2 1 +
1 +  2 = 2 ja
2 = 2 ja  '2-akselin yhtälö
'2-akselin yhtälö  1 -
1 -  2 + 3 = 0. Eräällä pisteellä on
koordinaatit
2 + 3 = 0. Eräällä pisteellä on
koordinaatit  1 = 1,
1 = 1,  2 = 2 ja
2 = 2 ja  '1 = -2,
'1 = -2,  '2 = 2. Millä pisteellä on samat koordinaatit
(
'2 = 2. Millä pisteellä on samat koordinaatit
( 1 =
1 =  '1,
'1,  2 =
2 =  '2) kummassakin koordinaatistossa?
'2) kummassakin koordinaatistossa?
Tehtävä 237
Tason kahden koordinaatiston väliset muunnoskaavat ovat
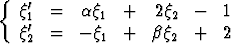 .
.
Yhtälöt  1 + 3
1 + 3 2 + 1 = 0 ja 2
2 + 1 = 0 ja 2 '1 -
'1 -  '2 + 5 = 0 esittävät samaa suoraa. Määritä
'2 + 5 = 0 esittävät samaa suoraa. Määritä  ja
ja
 .
.
Tehtävä 238
Kolmiossa ABC piste D puolittaa sivun BC, piste E sivun AC ja piste M on kolmion keskiö. Tarkastellaan koordinaatistoja {A,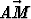 ,
, 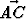 } ja {B,
} ja {B, 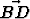 ,
, 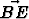 }. Erään
suoran yhtälö edellisessä koordinaatistossa on 2
}. Erään
suoran yhtälö edellisessä koordinaatistossa on 2 1 - 2
1 - 2 2 = 1. Määritä sen yhtälö
jälkimmäisessä koordinaatistossa. Piirrä kuvio.
2 = 1. Määritä sen yhtälö
jälkimmäisessä koordinaatistossa. Piirrä kuvio.
Tehtävä 239
Suunnikas ABCD (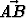
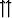
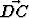 ), jonka keskipiste on M, määrää kaksi tason
koordinaatistoa: {A,
), jonka keskipiste on M, määrää kaksi tason
koordinaatistoa: {A, 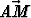 ,
, 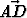 } ja {B,
} ja {B, 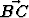 ,
, 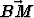 }. Muodosta koordinaatistonmuunnoskaavat.
Minkä pisteen koordinaatit säilyvät muuttumattomina siirryttäessä koordinaatistosta
toiseen? Piirrä kuvio.
}. Muodosta koordinaatistonmuunnoskaavat.
Minkä pisteen koordinaatit säilyvät muuttumattomina siirryttäessä koordinaatistosta
toiseen? Piirrä kuvio.
Tehtävä 240
Osoita, että vektorit b1 = i - 2k, b2 = 2i - j + 3k, b'1 = i + j - 9k ja b'2 = 5i - 2j + 4k ovat saman tason suuntaiset. Osoita, että sekä {O, b1, b2, b1 × b2} että {O, b'1, b'2, b'1 × b'2} voidaan valita avaruuden E3 koordinaatistoiksi; tässä on O o on
koordinaatistojen yhteinen origo. Määritä koordinaattimuunnoskaavojen matriisi
T .
o on
koordinaatistojen yhteinen origo. Määritä koordinaattimuunnoskaavojen matriisi
T .
Tehtävä 241
Tason E2 koordinaatisto {O, i, j} on siirretty ja kierretty uuteen asentoon {O' , i' , j' }; x’-akselin yhtälö pilkuttomissa koordinaateissa on x + 3y - 6 = 0, y’-akselin vastaavasti 3x - y - 4 = 0. Esitä koordinaattimuunnoskaavat kumpaankin suuntaan, kun lisäksi tiedetään, että i'- ja j-vektoreiden välinen kulma on terävä.Tehtävä 242
Koordinaatistoista {O, i, j, k} ja {O, i', j', k'} tiedetään seuraavaa: 1) Molemmat ovat ortonormeerattuja ja oikeakätisiä. 2) i' ja i + 2j + 2k ovat samansuuntaiset. 3) k' on xy-tason suuntainen siten, että kulma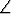 (k', i) on terävä. Lausu
koordinaatistonmuunnoskaava pilkuttomien koordinaattien suhteen ratkaistuna.
(k', i) on terävä. Lausu
koordinaatistonmuunnoskaava pilkuttomien koordinaattien suhteen ratkaistuna.
Tehtävä 243
Totea, että matriisi
T = 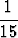
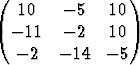
on ortogonaalinen. Määritä pisteet, joiden koordinaatit säilyvät ennallaan koordinaatistomuunnoksessa x' = T x.
5.7 Avaruuden  n geometriaa
n geometriaa
Tehtävä 244
Osoita, että avaruuden n vektorit
n vektorit
b1 =  , b2 =
, b2 =  , b3 =
, b3 =  , . . . , bn =
, . . . , bn = 
muodostavat avaruuden kannan.
Tehtävä 245
Olkoon x1, . . . , xn, y1, . . . , yn
 . Osoita:
. Osoita:
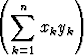 2 <
2 < 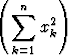
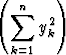 .
.
Tehtävä 246
Todista: ||x + y|| = ||x|| + ||y||, jos ja vain jos y = o tai x = y, missä
y, missä  > 0.
> 0.
Tehtävä 247
Todista Pythagoraan lause avaruudessa n: Jos x
n: Jos x 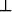 y, niin
||x - y||2 = ||x||2 + ||y||2.
y, niin
||x - y||2 = ||x||2 + ||y||2.
Tehtävä 248
Todista suunnikaslause avaruudessa n: ||x - y||2 + ||x + y||2 = 2||x||2 + 2||y||2.
Miksi lausetta sanotaan suunnikaslauseeksi?
n: ||x - y||2 + ||x + y||2 = 2||x||2 + 2||y||2.
Miksi lausetta sanotaan suunnikaslauseeksi?
Tehtävä 249
Todista: ||x|| = ||y||
 x + y
x + y 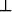 x - y.
x - y.
Tehtävä 250
Laske avaruuden 4 vektoreiden x =
4 vektoreiden x = 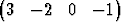 T ja y =
T ja y = 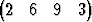 T
välisen kulman kosini. Mikä on kulman suuruus?
T
välisen kulman kosini. Mikä on kulman suuruus?
Tehtävä 251
Laske avaruuden 5 pisteiden P
5 pisteiden P 
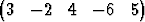 T ja
Q
T ja
Q 
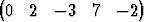 T välinen etäisyys.
T välinen etäisyys.
Tehtävä 252
Valitse jokin avaruuden 5 yksikkövektori x ja muodosta tämän avulla
matriisi H = I - 2xxT. Tutki, ovatko matriisin H pystyvektorit ortonormeeratut. Laske
vektorin x ja matriisin H pystyvektoreiden välisten kulmien kosinit ja itse kulmat.
5 yksikkövektori x ja muodosta tämän avulla
matriisi H = I - 2xxT. Tutki, ovatko matriisin H pystyvektorit ortonormeeratut. Laske
vektorin x ja matriisin H pystyvektoreiden välisten kulmien kosinit ja itse kulmat.
Tehtävä 253
Vektorit V b1 = i + 2j + 3k, b2 = i + 2j, b3 = i muodostavat avaruuden E3 kannan. Avaruus E3 varustetaan sisätulolla siten, että tämä kanta on ortonormeerattu, ts. sisätulolla on lauseke (u | v) = 1
1 1 +
1 +  2
2 2 +
2 +  3
3 3, missä luvut
3, missä luvut  1,
1,  2,
2,  3 ja
3 ja  1,
1,  2,
2,  3 ovat
vektoreiden u ja v koordinaatit em. kannassa. Esitä sisätulon lauseke kantaan {i, j, k}
liittyvien koordinaattien avulla. Totea, että lauseke voidaan kirjoittaa muotoon xTATAy,
missä A on sopiva matriisi. Laske vektoreiden j ja k täten määritelty sisätulo.
3 ovat
vektoreiden u ja v koordinaatit em. kannassa. Esitä sisätulon lauseke kantaan {i, j, k}
liittyvien koordinaattien avulla. Totea, että lauseke voidaan kirjoittaa muotoon xTATAy,
missä A on sopiva matriisi. Laske vektoreiden j ja k täten määritelty sisätulo.
Tehtävä 254
Olkoon F : n
n 
 n lineaarikuvaus. Osoita:
n lineaarikuvaus. Osoita:
(F (x) | F (y)) = 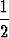
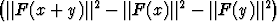 .
.
Päättele tämän avulla, että jos lineaarikuvaus säilyttää vektorien pituuudet
(ts. ||F (x)|| = ||x|| 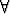 x), niin se säilyttää myös vektorien väliset kulmat (ts.
x), niin se säilyttää myös vektorien väliset kulmat (ts.
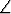 (F (x), F (y)) =
(F (x), F (y)) = 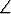 (x, y)
(x, y) 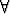 x, y).
x, y).