6 Suorien ja tasojen geometriaa
6.1 Suorien ja tasojen yhtälöt
Tehtävä 255
Osoita, että yhtälöt
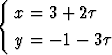 ja
ja 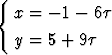
esittävät samaa tason suoraa.
Tehtävä 256
Määritä suoran
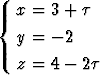
ja koordinaattitasojen leikkauspisteet.
Tehtävä 257
Määritä suorien
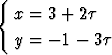 ja
ja 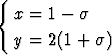
leikkauspiste.
Tehtävä 258
Millä luvun arvoilla suorat
arvoilla suorat
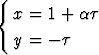 ja x - 2y + 5 = 0
ja x - 2y + 5 = 0
ovat yhdensuuntaiset?
Tehtävä 259
Määritä luku siten, että suorat
siten, että suorat
2(x - 1) = 1 - y = 2z - 3 ja 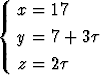
ja vektori i + 2j +  k ovat saman tason suuntaiset.
k ovat saman tason suuntaiset.
Tehtävä 260
Olkoon s1 xy-tason suora, jonka yhtälö on x + y - 1 = 0 ja olkoon s2 suora x = -y = z = . Määritä pisteet P1
. Määritä pisteet P1  s1 ja P2
s1 ja P2  s2 siten, että vektori
s2 siten, että vektori 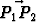 on
yhdensuuntainen vektorin i - j + k kanssa.
on
yhdensuuntainen vektorin i - j + k kanssa.
Tehtävä 261
Kolmion kaksi kärkeä ovat origo ja piste (2, 2, -1). Yksi sivu on suoralla x = 2y = z. Määritä kolmas kärki, kun kolmannen sivun tiedetään olevan i - j + k,
missä
k,
missä  on eräs luku. Mikä luku
on eräs luku. Mikä luku  on?
on?
Tehtävä 262
Suora s kulkee pisteen (-1, 1, 3) ja sen janan keskipisteen kautta, jonka zx- ja xy-tasot leikkaavat suorasta x - 1 = 2(y + 1) = z + 3. Määritä suoran s suuntavektori.Tehtävä 263
Määritä siten, että suorat 2(x - 1) = y + 1 = 2
siten, että suorat 2(x - 1) = y + 1 = 2 (z - 1) ja x + 1 = y - 1 = z
leikkaavat.
(z - 1) ja x + 1 = y - 1 = z
leikkaavat.
Tehtävä 264
Tason koordinaatistosta {O, b1, b2} tiedetään, että |b1| : |b2| = . Tämän
koordinaatiston pisteen (1, 1) kautta kulkeva suora leikkaa koordinaattiakselit (so. origon
kautta kulkevat kantavektoreriden suuntaiset suorat) pisteissä A ja B siten, että
|
. Tämän
koordinaatiston pisteen (1, 1) kautta kulkeva suora leikkaa koordinaattiakselit (so. origon
kautta kulkevat kantavektoreriden suuntaiset suorat) pisteissä A ja B siten, että
|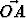 | = |
| = |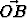 |. Missä pisteessä tämä suora leikkaa suoran
|. Missä pisteessä tämä suora leikkaa suoran  -
-  + 3 = 0 (so. suoran, jonka
pisteiden koordinaatit (
+ 3 = 0 (so. suoran, jonka
pisteiden koordinaatit ( ,
,  ) toteuttavat em. yhtälön)? Piirrä kuvio tapauksessa b1 = i,
b2 = i + j.
) toteuttavat em. yhtälön)? Piirrä kuvio tapauksessa b1 = i,
b2 = i + j.
Tehtävä 265
Taso kulkee pisteiden (0, 2, 1) ja (-3, 4, 1) kautta sekä on vektorin 2i - k suuntainen. Määritä tason yhtälö parametrimuodossa.Tehtävä 266
Tason parametrimuotoinen yhtälö on
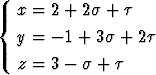 .
.
Esitä yhtälö muodossa ax + by + cz = d. Mikä on tason normaalivektori?
Tehtävä 267
Osoita, että piste P 3i - j + 2k sijaitsee tasossa, joka kulkee pisteen
P0
3i - j + 2k sijaitsee tasossa, joka kulkee pisteen
P0  i - 13j - 5k kautta ja on vektoreiden s = i - j ja t = i + j + k suuntainen.
i - 13j - 5k kautta ja on vektoreiden s = i - j ja t = i + j + k suuntainen.
Tehtävä 268
Taso kulkee pisteiden (1, -1, 2) ja (3, 1, 2) kautta sekä on vektorin 2i + 3j - k suuntainen. Määritä tason yhtälö muodossa ax + by + cz = d.Tehtävä 269
Määritä muodossa ax + by + cz = d sen tason yhtälö, joka kulkee suoran
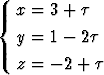
kautta sekä a) pisteen (0, 2, 1) kautta, b) on vektorin 3i + j - 2k suuntainen.
Tehtävä 270
Määritä tasojen 2x - y + 2z = 5 ja 2x + 3y - 5z + 7 = 0 yhteiset pisteet.Tehtävä 271
Millä arvoilla ,
,  ,
, 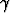 tasot x +
tasot x +  y +
y +  z = 2
z = 2 -
- 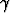 + 1 ja
+ 1 ja
 x + (
x + ( + 2)y +
+ 2)y + 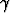 z = 2
z = 2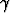 +
+  ovat yhdensuuntaiset? Voidaanko luvut valita siten, että
tasot yhtyvät?
ovat yhdensuuntaiset? Voidaanko luvut valita siten, että
tasot yhtyvät?
Tehtävä 272
Määritä seuraavien tasojen yhteiset pisteet:| a) x + y - z + 2 = 0, 2x + y + 2z - 4 = 0, x + 3z - 2 = 0, | |||
| b) x + y + z - 6 = 0, x + 2y - z - 2 = 0, 2x - y + z - 3 = 0. |
Tehtävä 273
Olkoon annettuna kaksi suoraa parametriesityksen avulla:
r = (1 +  )i + (1 + 2
)i + (1 + 2 )j + (1 + 3
)j + (1 + 3 )k ja r = (1 +
)k ja r = (1 +  )i + (-1 +
)i + (-1 +  )j + k.
)j + k.
Esitä muodossa ax + by + cz = d sen tason yhtälö, joka kulkee edellisen suoran kautta ja on jälkimmäisen suuntainen; esitä vastaavasti jälkimmäisen suoran kautta kulkeva edellisen suoran suuntainen taso.
Tehtävä 274
Suoran x = 3 + 2 , y = -2 +
, y = -2 +  , z = 1 -
, z = 1 -  kautta asetetaan taso, joka on
vektorin i - j - k suuntainen. Esitä taso sekä parametrimuodossa että yhden yhtälön
avulla. Mikä on tason normaalivektori?
kautta asetetaan taso, joka on
vektorin i - j - k suuntainen. Esitä taso sekä parametrimuodossa että yhden yhtälön
avulla. Mikä on tason normaalivektori?
Tehtävä 275
Johda sen tason yhtälö, joka puolittaa pisteen P0 (x0, y0, z0) ja tason
T (x, y, z) = 0 väliset janat.
(x0, y0, z0) ja tason
T (x, y, z) = 0 väliset janat.
Tehtävä 276
Olkoon {O, b1, b2, b3} avaruuden E3 koordinaatisto. Olkoon annettuna taso T ja suora s parametrimuotoisten yhtälöiden avulla:
r = 2ub1 + vb2 + ub3, r = (1 + 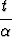 )b1 + (t - 2)b2 + (2
)b1 + (t - 2)b2 + (2 - t)b3,
- t)b3,
missä u, v, t ovat parametrit ja  on vakio. Määritä
on vakio. Määritä  siten, että tason T ja suoran s
leikkauspiste puolittaa vektoreiden b1, b2 ja b2, b3 määräämien koordinaattitasojen
suorasta s leikkaaman janan.
siten, että tason T ja suoran s
leikkauspiste puolittaa vektoreiden b1, b2 ja b2, b3 määräämien koordinaattitasojen
suorasta s leikkaaman janan.
Tehtävä 277
Koordinaatiston {O, b1, b2, b3} kantavektoreista tiedetään, että |b1 | : |b2 | : |b3| = 2 : 3 : 5. Taso T kulkee pisteen (1, 1, 1) kautta ja leikkaa positiiviset koordinaattiakselit pisteissä, joiden etäisyydet origosta ovat yhtä suuret. Johda em. koordinaatistossa tason T yhtälö ja määritä piste, jossa origon kautta kulkeva vektorin 2b1 + 3b2 + 5b3 suuntainen suora leikkaa sen.Tehtävä 278
Osoita, että pisteiden (xk, yk, zk), k = 1, 2, 3, (jotka eivät ole samalla suoralla) kautta kulkevan tason yhtälö voidaan kirjoittaa muotoon
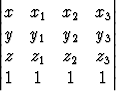 = 0.
= 0.
Tehtävä 279
Määritä suorilta
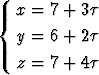 ja
ja 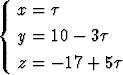
sellaiset pisteet, että niiden yhdysjana on kohtisuorassa molempia suoria vastaan. Esitä yhteisen normaalin parametrimuotoinen yhtälö.
Tehtävä 280
Määritä pisteen (3, 4, -2) kohtisuora projektio sillä tasolla, joka kulkee pisteen (1, 0, -1) kautta ja on kohtisuorassa vektoria i - 2j + k vastaan.Tehtävä 281
Määritä pisteen (3, 4, -2) kohtisuora projektio tasolla
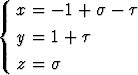 .
.
Tehtävä 282
Määritä ne suorat, jotka leikkaavat suorat
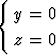 ,
, 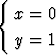
sekä muodostavat kummankin kanssa 60o kulman.
Tehtävä 283
Määritä sen tason yhtälö, joka on suorien
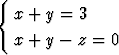 ja
ja 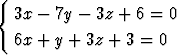
suuntainen ja yhtä etäällä näistä.
Tehtävä 284
Laske tasojen 2x + y - 2z - 4 = 0 ja 3x + 6y - 2z - 12 = 0 välisen terävän diedrikulman kosini.Tehtävä 285
Määritä tasojen x + 2y + 3z = 1 ja r = i - (i - 3k) -
(i - 3k) -  (j - 2k) välinen
(pienempi) kulma asteen tarkkuudella. Määritä jokin piste tasojen leikkaussuoralta ja
suoran suuntavektori.
(j - 2k) välinen
(pienempi) kulma asteen tarkkuudella. Määritä jokin piste tasojen leikkaussuoralta ja
suoran suuntavektori.
Tehtävä 286
Määritä pisteen (3, 2, -4) symmetrinen piste tason x + y - 2z + 5 = 0 suhteen.Tehtävä 287
Määritä pisteen (3, 2, 1) symmetrinen piste suoran x - 1 = 2(1 - y) = z + 3 suhteen.Tehtävä 288
Määritä origon suurin mahdollinen etäisyys pisteiden (0, 1, 0) ja (1, 0, 2) kautta kulkevasta tasosta. Mikä taso antaa maksimietäisyyden?Tehtävä 289
Tarkastellaan niitä tason x + 2y + z - 3 = 0 pisteitä, joiden kohtisuora projektio suoralla x + 1 = y - 1 = z on (2, 4, 3). Määritä näistä se, joka on lähinnä origoa.Tehtävä 290
Määritä se suoran r = i + 2j + (-i + k) tasolla x + 2y + 2z = 0 olevan
kohtisuoran projektion piste, jonka kohtisuora projektio suoralla x = y = z on
origo.
(-i + k) tasolla x + 2y + 2z = 0 olevan
kohtisuoran projektion piste, jonka kohtisuora projektio suoralla x = y = z on
origo.
Tehtävä 291
Määritä suoran
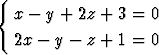
xy-tasolla olevan kohtisuoran projektion ja tason x - y - z + 1 = 0 välisen kaltevuuskulman sini.
Tehtävä 292
Vektorin 2i - j + 3k kanssa samansuuntainen valonsäde kohtaa heijastavan tason pisteessä (1, 2, -1). Heijastunut säde kulkee pisteen (2, 5, -3) kautta. Johda tason yhtälö.Tehtävä 293
Positiivisen z-akselin suunnasta tuleva valonsäde osuu pisteessä (1, 2, 3) tasolla 3x + 2y + z = 10 olevaan peiliin ja heijastuu tästä. Määritä heijastuneen säteen suunta. Kohtaako heijastunut säde xy-tasoa? Jos, niin missä pisteessä?Tehtävä 294
Painovoima vaikuttakoon negatiivisen z-akselin suuntaan. Pisara putoaa pisteestä (1, 1, 3) tasolle 3x - 4y + 12z = 12 ja alkaa valua tasoa pitkin alaspäin. Missä pisteessä se kohtaa xy-tason?Tehtävä 295
Määritä pisteen (2, -3, 1) kohtisuora projektio suoralla
a) r = 2i + 3j - k +  (2i + 2j + k), b)
(2i + 2j + k), b) 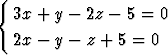 .
.
Tehtävä 296
Laske pisteen (2, 3, -1) etäisyys suorasta
a) r = i + 2j + 3k +  (i - 2j + 2k), b)
(i - 2j + 2k), b) 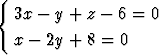
Tehtävä 297
Määritä suorien
r = (i + 2j + 3k) +  (i - 2j + 2k) ja
(i - 2j + 2k) ja 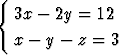
lyhin etäisyys.
Tehtävä 298
Määritä suorien
r = (2i + 5k) +  (i - 2j + 2k) ja
(i - 2j + 2k) ja 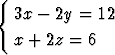
lyhin etäisyys ja lähinnä toisiaan olevat pisteet.
Tehtävä 299
Massapisteistön hitausmomentti on J =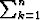 mkd
mkd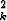 , missä indeksi k numeroi
pisteet, mk on pisteen massa ja dk sen kohtisuora etäisyys pyörähdysakselista. Pisteessä
(3, 2, 1) on massa 5 ja pisteessä (3, 1, 4) massa 17. Laske hitausmomentti, kun akselina on
suora 5x = 3y = 2z. Tarkka arvo ja likiarvo.
, missä indeksi k numeroi
pisteet, mk on pisteen massa ja dk sen kohtisuora etäisyys pyörähdysakselista. Pisteessä
(3, 2, 1) on massa 5 ja pisteessä (3, 1, 4) massa 17. Laske hitausmomentti, kun akselina on
suora 5x = 3y = 2z. Tarkka arvo ja likiarvo.
Tehtävä 300
Olkoot a, b ja c kolme nollasta eroavaa avaruuden E3 vektoria. Tutki, millä ehdolla pistejoukko { P r | (a × r) × b = c } on a) tyhjä, b) suora,
c) taso.
r | (a × r) × b = c } on a) tyhjä, b) suora,
c) taso.
Tehtävä 301
Osoita, että tasot 2x + y + z - 1 = 0, x - 2y = 0 ja 2x + y - 5z + 5 = 0 voidaan valita uuden ortonormeeratun oikeakätisen koordinaatiston y’z’-, z’x’- ja x’y’-tasoiksi. Johda koordinaattien muunnoskaavat, kun tiedetään, että pisteen (x, y, z) = (1, -1, 1) uudet koordinaatit (x', y', z') ovat positiiviset.Tehtävä 302
Pistejoukko
s = { x | x = 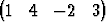 T +
T + 
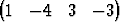 T }
T }
on avaruuden  4 hypersuora ja pistejoukko
4 hypersuora ja pistejoukko
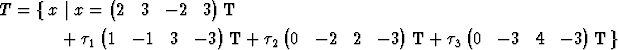
sen kolmiulotteien hypertaso. Laske suoran s ja tason T leikkauspiste.
Tehtävä 303
Todista, että hypertasotx = 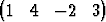 T + T +  1 1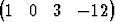 T + T +  2 2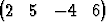 T ja T ja | |||
x = 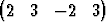 T + T +  1 1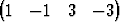 T + T +  2 2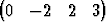 T + T +  3 3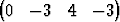 T T |
ovat yhdensuuntaiset. (Vertaa: Milloin avaruudessa E3 suora on tason suuntainen?)
Tehtävä 304
Todista, että hypersuora
x = 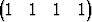 T +
T + 
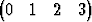 T
T
ei ole hypertason
x = 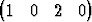 T +
T +  1
1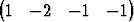 T +
T +  2
2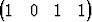 T
T
suuntainen. Onko näillä leikkauspisteitä?
Tehtävä 305
Määritä dimensioltaan pienin hypertaso, joka sisältää pisteetP1  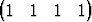 T, T, | P2  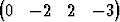 T, T, | ||||||
P3  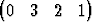 T, T, | P4  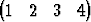 T. T. |
6.2 Painopistekoordinaatit
Tehtävä 306
Suora kulkee pisteiden P1 (2, 1, 3) ja P2
(2, 1, 3) ja P2  (-1, 2, 1) kautta. Tutki,
ovatko pisteet (8, -1, 5) ja (-7, 4, -3) suoralla. Määritä myönteisessä tapauksessa
painopistekoordinaatit ja päättele näistä pisteen sijainti pisteisiin P1 ja P2 nähden.
(-1, 2, 1) kautta. Tutki,
ovatko pisteet (8, -1, 5) ja (-7, 4, -3) suoralla. Määritä myönteisessä tapauksessa
painopistekoordinaatit ja päättele näistä pisteen sijainti pisteisiin P1 ja P2 nähden.
Tehtävä 307
Kolmion kärjet ovat A (
( , 0), B
, 0), B  (
( , 0) ja C
, 0) ja C  (0,
(0, 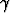 ). Johda keskijanojen
parametrimuotoiset yhtälöt.
). Johda keskijanojen
parametrimuotoiset yhtälöt.
Tehtävä 308
Tutki, ovatko pisteet ( , -
, - ), (
), ( +
+  ,
,  -
-  ) ja (
) ja ( + 2
+ 2 , 2
, 2 -
-  ) samalla
suoralla.
) samalla
suoralla.
6.3 Suora- ja tasoparvista
Tehtävä 309
Määritä tason suorien
(1 + 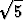 )x - (7 -
)x - (7 - 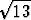 )y = 1 ja (2 -
)y = 1 ja (2 - 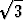 )x + (4 -
)x + (4 - 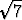 )y = 2
)y = 2
leikkauspisteen ja origon kautta kulkevan suoran yhtälö.
Tehtävä 310
Määritä suorien3x - y + 1 = 0 ja x + 2y - 2 = 0
leikkauspisteen kautta kulkeva suora, joka a) kulkee pisteen (2, -1) kautta, b) on vektorin i - 2j suuntainen.
Tehtävä 311
Määritä tason suorien y = 7x ja x + y = 8 leikkauspisteen kautta kulkevat suorat, joiden etäisyys origosta on 5.Tehtävä 312
Kolmion sivut ovat tason suorilla y = 0, 3x + 4y = 12 ja 5x = 12y. Määritä kulmanpuolittajat, niiden leikkauspiste ja sisäänpiirretyn ympyrän säde.Tehtävä 313
Määritä tasojen x + y + z = 3 ja 3x - 2y + z = 7 leikkaussuoran sekä origon kautta kulkevan tason yhtälö.Tehtävä 314
Määritä se tasojen x + y + z = 2 ja x + 2y - z = 1 leikkaussuoran kautta kulkeva taso, joka sisältää pisteen (1, 1, 1).Tehtävä 315
Määritä tasojen 3x - 5y + z + 9 = 0 ja x - 3y - 5z - 1 = 0 välisten diedrikulmien puolittajatasot.Tehtävä 316
Määritä se tasojen x + y + z = 2 ja x + 2y - z = 1 leikkaussuoran kautta kulkeva taso, joka on suoran
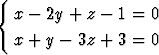
suuntainen.
Tehtävä 317
Määritä luvut ja
ja  siten, että tasot 3x + 3y - 4z + 7 = 0,
x + 6y + 2z - 6 = 0 ja x +
siten, että tasot 3x + 3y - 4z + 7 = 0,
x + 6y + 2z - 6 = 0 ja x +  y +
y +  z = 0 kulkevat saman suoran kautta. Esitä suoran yhtälö
parametrimuodossa.
z = 0 kulkevat saman suoran kautta. Esitä suoran yhtälö
parametrimuodossa.
Tehtävä 318
Johda sen tason yhtälö, joka jakaa tasojen x - 2y + z = 2 ja 3x - 6y + 3z = 17 väliset janat suhteessa 2 : 3.Tehtävä 319
Määritä tasojen x = 2y + 3 ja y + z + 3 = 0 leikkaussuoran kautta kulkeva taso, joka puolittaa ne tasojen yhdysjanat, jotka ovat suoran 2x = 2y = -z suuntaiset.Tehtävä 320
Suoran
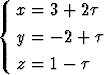
kautta asetetaan taso, joka on vektorin -i + j + k suuntainen. Määritä tämän tason ja z-akselin leikkauspiste.
Tehtävä 321
Koordinaatiston {O, b1, b2, b3} kantavektoreista tiedetään, että |b1| = |b2|. Määritä ne suoran r = (1 + )b1 + (3 -
)b1 + (3 -  )b2 + (2 +
)b2 + (2 +  )b3 kautta kulkevat tasot, jotka
leikkaavat b1 - ja b2-koordinaattiakselit yhtä etäällä origosta.
)b3 kautta kulkevat tasot, jotka
leikkaavat b1 - ja b2-koordinaattiakselit yhtä etäällä origosta.
Tehtävä 322
Määritä suoran
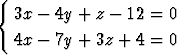
kautta kulkevat tasot, joiden etäisyys origosta on 4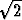 .
.