7 Matriisin ominaisarvot
7.1 Ominaisarvon ja ominaisvektorin käsite; laskeminen
Tehtävä 323
Olkoon matriisin A ominaisarvo ja olkoon x
matriisin A ominaisarvo ja olkoon x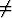 o vastaava ominaisvektori.
Osoita, että matriisilla Ap on ominaisarvona
o vastaava ominaisvektori.
Osoita, että matriisilla Ap on ominaisarvona  p ja vastaava ominaisvektori on x
(p
p ja vastaava ominaisvektori on x
(p 
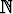 ).
).
Tehtävä 324
Neliömatriisi A olkoon säännöllinen (ts. käänteismatriisi A-1 on olemassa) ja
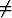 0 olkoon sen ominaisarvo, x
0 olkoon sen ominaisarvo, x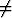 o vastaava ominaisvektori. Todista: käänteismatriisilla
on ominaisarvo 1/
o vastaava ominaisvektori. Todista: käänteismatriisilla
on ominaisarvo 1/ ja vastaava ominaisvektori on x.
ja vastaava ominaisvektori on x.
Tehtävä 325
Osoita muodostamatta polynomiyhtälöä ominaisarvoille, että matriisin
A = 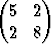
ominaisvektorit ovat x1 = 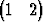 T ja x2 =
T ja x2 = 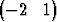 T. Mitkä ovat vastaavat
ominaisarvot?
T. Mitkä ovat vastaavat
ominaisarvot?
Tehtävä 326
Osoita oikeaksi tai vääräksi: Jos 1 ja
1 ja  2 ovat matriisin A ominaisarvoja
(
2 ovat matriisin A ominaisarvoja
( 1
1 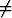
 2 ), niin
2 ), niin  1 +
1 +  2 on matriisin A ominaisarvo.
2 on matriisin A ominaisarvo.
Tehtävä 327
Matriisilla
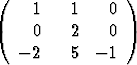
on ominaisvektoreina 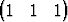 T,
T, 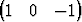 T ja
T ja 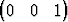 T. Olkoon x =
T. Olkoon x = 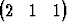 T.
Laske A11 x.
T.
Laske A11 x.
Tehtävä 328
Laske matriisin
A = 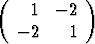
ominaisarvot ja -vektorit. Voidaanko ominaisvektorit valita ortonormeeratuiksi?
Tehtävä 329
Laske matriisin
A = 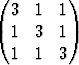
ominaisarvot ja -vektorit.
Tehtävä 330
Tutki matriisin
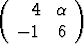
ominaisarvoja ja -vektoreita parametrin  eri arvoilla. Mitä voidaan sanoa niiden
reaalisuudesta ja kompleksisuudesta? Montako lineaarisesti riippumatonta ominaisvektoria
voidaan löytää?
eri arvoilla. Mitä voidaan sanoa niiden
reaalisuudesta ja kompleksisuudesta? Montako lineaarisesti riippumatonta ominaisvektoria
voidaan löytää?
Tehtävä 331
Määritä matriisin
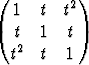
ominaisarvot parametrin t funktioina ja piirrä näiden kuvaajat.
Tehtävä 332
Määritä matriisin
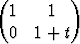
ominaisvektoreiden välinen kulma parametrin t funktiona. Mitä tämä kertoo ominaisvektoreiden lineaarisesta riippumattomuudesta?
Tehtävä 333
Olkoon matriisin
matriisin
A = 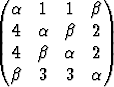
ominaisarvo. Millä lukuja  ,
,  ,
,  koskevalla ehdolla matriisilla on ominaisvektorina
koskevalla ehdolla matriisilla on ominaisvektorina
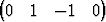 T ?
T ?
7.2 Diagonalisointi; symmetriset matriisit
Tehtävä 334
Määritä matriisin
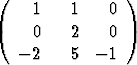
ominaisarvot ja -vektorit. Onko matriisi diagonalisoituva? Ilmoita myönteisessä tapauksessa vastaava diagonaalimatriisi ja similariteettimuunnosmatriisi.
Tehtävä 335
Määritä seuraavan matriisin ominaisarvot ja -vektorit sekä tutki sen diagonalisoituvuutta:
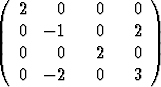 .
.
Tehtävä 336
Laske matriisien
a) 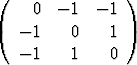 , b)
, b) 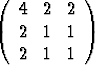 , c)
, c) 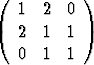
ominaisarvot ja ominaisvektorit. Muodosta ominaisvektoreista ortonormeerattu kanta.
Tehtävä 337
Laske matriisien
a) A = 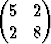 , b) A =
, b) A = 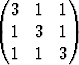
ominaisarvot ja ominaisvektorit. Muodosta ortogonaalinen similaritettimuunnosmatriisi
T (so. matriisi, jolle pätee T -1 = T T). Kirjoita vastaava lävistäjämatriisi  ja totea, että
T -1 AT =
ja totea, että
T -1 AT =  .
.
Tehtävä 338
Tutki similariteettimuunnosta seuraavien matriisien tapauksessa:
a) 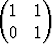 , b)
, b) 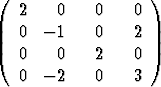 , c)
, c) 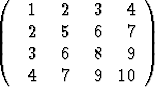 .
.
Ovatko matriisit diagonalisoituvia? Totea myönteisessä tapauksessa yhtälön T -1AT =  voimassaolo numeerisella laskulla.
voimassaolo numeerisella laskulla.
7.3 Neliömuodot
Tehtävä 339
Kirjoita neliömuodona) Q(x, y) = 16x2+9y2+24xy, b) Q(x, y) = xy, c) Q(x, y, z) = x2+y2+z2+xy+yz+zx
esitysmatriisi, hae sen ominaisarvot ja luokittele neliömuoto.
Tehtävä 340
Muodosta neliömuodon Q(x, y, z) = x2 + y2 + z2 + 2xy + 2yz + 2zx esitysmatriisi. Määritä tämän ominaisarvot ja ortonormeeratut ominaisvektorit. Millaisten lävistäjämatriisen kanssa esitysmatriisi on similaarinen? Luokittele neliömuoto.Tehtävä 341
Luokittele seuraavat neliömuodot:| a) | Q(x, y, z) = (x + y)2 + (y + z)2 + (z + x)2, | ||
| b) | Q(x, y, z) = (x + 3y - z)2 + (x - y - z)2 + (x + y - z)2. |
Tehtävä 342
Tutki, missä xy-tason pisteissä seuraavat neliömuodot saavat arvon 0:| a) | Q(x, y) = 2x2 + 3y2 + 2xy, | ||
| b) | Q(x, y) = x2 + 4y2 + 4xy, | ||
| c) | Q(x, y) = 3x2 + y2 + 4xy. |