8 Geometriset kuvaukset

8.1 Euklidiset kuvaukset

Tehtävä 344

Esitä muodossa x' = Ax + b se avaruuden E³ peilauskuvaus, jonka symmetriatasona on 2x₁ - 3x₂ + x₃ = 6.

Tehtävä 345

Tason kiertokuvauksen kiertokulma on 60^o (positiiviseen suuntaan) ja kierron keskipiste (2, 3). Esitä kiertokuvaus muodossa x' = Ax + b, so. määritä matriisi A ja pystyvektori b. Laske sen neliön kuva, jonka kärkinä ovat (0, 0), (1, 0), (1, 1) ja (0, 1).

Vastaus

Tehtävä 346

Osoita, että kaikki paraabelit ovat yhdenmuotoisia etsimällä skaalauskuvaus, joka vie paraabelin y = ax² paraabelille y = bx².

Tehtävä 347

Yhtälö x' = Ax + b, missä

A = 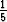( - 3 4 )

4 3 , b = ( -2 )

1 ,

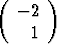esittää tason euklidista kuvausta. Tutki, millainen kuvaus on kyseessä.

Vastaus

Tehtävä 348

Kuvaus

( )
x'
y' = 1
---
25 ( )
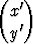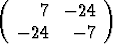
7 - 24
- 24 - 7 ( )
x
y

kuvaa xy-tason pisteet xy-tason pisteiksi. Osoita, että kyseessä on peilauskuvaus ja määritä sen akseli. Laske kolmion ABC kuva, kun A (0, 0), B (5, 1) ja C (0, -2). Piirrä kuvio.

Tehtävä 349

Kolmiulotteisen avaruuden kierron akseli kulkee origon kautta ja sen suuntavektori on i + 2j + 3k; kiertokulma on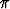

/6 radiaania. Laske numeerisesti kiertokuvauksen matriisi.

Vastaus

Tehtävä 350

Yksikkösärmäisen kuution yksi kärki on origossa ja tästä lähtevät särmät positiivisilla koordinaattiakseleilla. Kuutiota kierretään toistuvasti edellisen tehtävän kierrolla. Muodosta kiertomatriisi ja laske kierrettyjen kuutioiden kärjet. Piirrä kierretyt kuutiot projisioituina xy-tasoon. Piirtäminen helpottuu, jos alkuperäisen kuution kärkien koordinaatit asetetaan 3 × n-kokoisen matriisin pystyvektoreiksi sellaiseen järjestykseen, että kärjet yhdistämällä saadaan piirretyksi koko kuutio; tällöin joudutaan eräissä kärjissä käymään useampaan kertaan, jolloin matriisissa on useampia pystyvektoreita kuin kuutiossa on kärkiä. Kierrettyjen kuutioiden kärkipisteille saadaan tämän jälkeen vastaavanlaiset koordinaattimatriisit matriisitulon avulla.

Tehtävä 351

Kolmiulotteisen avaruuden kierron akseli kulkee origon kautta ja sen suuntavektori on 2i - j + 4k; kiertokulma on 0.1 radiaania. Laske kiertokuvauksen matriisi. Kierrä tämän avulla toistuvasti pistettä (1, 0, 0) ja piirrä täten syntyvien pisteiden xy-tasoon otetut ortogonaaliprojektiot. Millaisella käyrällä projektiopisteet sijaitsevat?

Tehtävä 352

Skaalaa edellisen tehtävän kierron suuntavektori siten, että sen pituus on sama kuin kiertokulman suuruus. Muodosta täten skaalattua vektoria vastaava ristitulomatriisi N^× ja laske numeerisesti e^{N^×} jollakin tietokoneohjelmalla. Mitä kiertoon liittyvää saat? (Kyseessä on matriisieksponenttifunktio, jonka argumentin tulee olla neliömatriisi. Tarkempi käsittely esitetään matriisilaskun oppikirjoissa.)

Tehtävä 353

Olkoot T_a ja T_b kaksi translaatiota. Osoita, että nämä kommutoivat, ts. T_a o T_b = T_b o T_a.

Tehtävä 354

Olkoot U ja U tason E² kiertokuvauksia, joiden keskuksena on origo. Osoita, että nämä kommutoivat, ts. UoU = UoU. Päteekö sama kahdelle avaruuden E³ kiertokuvaukselle, joiden keskuksena on origo?

Tehtävä 355

Olkoon T_a tason translaatio ja U tason kiertokuvaus keskuksena origo. Osoita esimerkillä, että välttämättä ei ole T_aoU = UoT_a. Millä ehdolla yhtälö on voimassa?

Vastaus

Tehtävä 356

Esitä analyyttisesti se tason E² euklidinen kuvaus, joka kuvaa kolmion ABC kolmiolle A' B'C', kun A

(7, -1), B

(6, -1), C

(6, -3), A'

(-1, 1), B'

(-1, 2), C'

(-3, 2). Minne kuvautuu piste P

(1, 1)?

Vastaus

Tehtävä 357

Olkoot P₁

(x₁, y₁) ja P₂

(x₂, y₂) tason E² pisteitä, d näiden etäisyys. Esitä analyyttisesti tason euklidinen liike, joka kuvaa janan P₁P₂ janalle {(x, 0) | 0 < x < d}. Onko tulos yksikäsitteinen?

Vastaus

8.2 Yhdensuuntaisprojektio

Tehtävä 358

Yhdensuuntaisprojektion matriisi on

P = 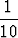1
---
10 ( )
7 - 6 - 9
- 2 6 - 6
- 1 - 2 7 .

Määritä kuvatason yhtälö ja projektiosäteen suuntavektori. Onko kyseessä ortogonaaliprojektio?

Tehtävä 359

Matriisi

P = 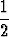1
--
2 ( )
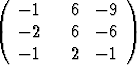
- 1 6 -9
- 2 6 -6
- 1 2 -1

esittää yhdensuuntaisprojektiota. Määritä matriisin ominaisarvot ja -vektorit. Määritä yhdensuuntaisprojektion kuvataso ja projektiosäteen suunta. Miten nämä saadaan ominaisvektoreiden avulla?

Tehtävä 360

Taso E² projisioidaan vektorin -2i + j suuntaan suoralle x₂ = 3x₁. Esitä kuvaus muodossa x' = P x, ts. määritä matriisi P . Onko tällä ominaisuus P ² = P ? Mitkä pisteet kuvautuvat pisteelle (1, 3)?

Vastaus

Tehtävä 361

Dimetrinen ortogonaaliprojektio on yhdensuuntaisprojektio, jonka kuvataso on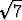 V~
7

x + y + z = 0. Johda kaavat yhdensuuntaisprojektiokuvan laskemista varten.

Tehtävä 362

Laske ja piirrä edellisen tehtävän kaavoja käyttäen ruuviviivan

r(t) = cos t i + sin t j + at k

kuva dimetrisessä ortogonaaliprojektiossa. Valitse ruuviviivan nousuksi a = 0.1.

Tehtävä 363

Kokeile erilaisia ruuviviivan nousuja edellisen tehtävän ortogonaaliprojektiokuvassa. Miten nousu on valittava, jotta projektiokäyrällä olisi kärkiä? Miten tämä nousu voidaan laskea?

8.3 Affiniteetti

Tehtävä 364

Suorakulmion kärjet ovat (1, 1), (3, 1), (3, 2), (1, 2). Laske suorakulmion affiininen kuva, kun affiniteetin esityksessä on

A = ( )
1 2
3 4 , b = ( )
5
6 .

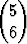Laske suorakulmion ja sen kuvan pinta-alojen suhde. Miten tämä suhtautuu matriisin A determinanttiin? Piirrä kuvio.

Tehtävä 365

Olkoon

A = ( )
1 1
1 2 , b = ( )
2
3 ,

jolloin yhtälö x' = Ax + b määrittää tason E² affiinin kuvauksen itseensä. Määritä sen käyrän yhtälö, joksi yksikköympyrä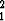 x + x = 1 kuvautuu tässä kuvauksessa. Piirrä kuvakäyrä.

Tehtävä 366

Olkoon x' = Ax + b affiininen kuvaus tasosta E² tasoon E² tai avaruudesta E³ avaruuteen E³; olkoon matriisi A säännöllinen (ts. käänteismatriisi on olemassa). Osoita, että kuvaus kuvaa suoran suoraksi. Missä kohden tarvitaan oletusta, että matriisi A on säännöllinen?

8.4 Keskusprojektio

Tehtävä 367

Keskusprojektion kuvataso on yz-taso ja projektiokeskus sijaitsee pisteessä (5, 0, 0). Muodosta kaavat keskusprojektiokuvan laskemista varten. Laske ja piirrä sen kuution perspektiivikuva (keskusprojektiokuva), jonka pisteille pätee -3 < x < 0, -1 < y < 2, 0 < z < 3.

Vastaus

Tehtävä 368

Pisteestä (0, 0, 5) katsellaan vektorin i + 2j suuntaan. Johda kaavat syntyvän perspektiivikuvan (keskusprojektiokuvan) laskemiseksi.

8.5 Projektiviteetti

Tehtävä 369

Tutki, miten projektiviteetti

x₁' = -3x1---2x2-
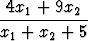
x1 + x2 + 5 , x₂' = 4x1-+--9x2-
x1 + x2 + 5

kuvaa tasoalueen { (x₁, x₂) | x₁ > 0, x₂ > 0 }. Piirrä kuva.

Tehtävä 370

Tutki, millaisiksi käyriksi ympyrät kuvautuvat tason kuvauksessa

x₁' = -x2 +-1-
x1 + x2 , x₂' = -x1-+-1-
x1 + x2 .

Tutki erityisesti ympyröitä, joiden keskipisteet ja säteet ovat seuraavat:

a) (2, 3), r = 2; b) (-2, 0), r = 1; c) (1, 1), r = 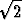V~ --
2 ; d) (0, 0), r = 2.

Millaisia käyriä näiden kuvat ovat? Muodosta ensin kuvattavalle ympyrälle tavanomainen ympyrän parametriesitys x₁ = a + r cos , x₂ = b + r sin , ja laske tämän avulla kuvakäyrän parametriesitys.