9 Toisen asteen käyrät ja pinnat
9.1 Käyrän ja pinnan käsitteet
Tehtävä 371
Piirrä seuraavat käyrät:
a) 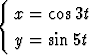 , t
, t  [0, 2
[0, 2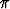 ], b)
], b) 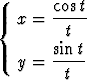 , t > 0.
, t > 0.
Tehtävä 372
Lausu napakoordinaattikäyrät a) r cos( -
- 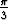 ) = 2, b) r = 2a cos
) = 2, b) r = 2a cos  ,
c) r = 2a sin
,
c) r = 2a sin  xy-koordinaatistossa.
xy-koordinaatistossa.
Tehtävä 373
Piirrä seuraavat pinnat:
a) 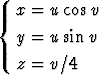 , u
, u  [0, 2], v
[0, 2], v  [0, 8
[0, 8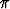 ], b)
], b) 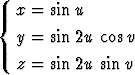 , u
, u  [-
[-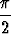 ,
, 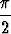 ], v
], v  [0, 2
[0, 2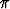 ].
].
9.2 Kartioleikkaukset
Tehtävä 374
Suoran ympyräkartion muodostajasuoran ja kartion pohjaympyrän välinen kulma on 45o . Kartiota leikataan tasolla, jonka kaltevuuskulma on , 0 <
, 0 <  < 45o. Laske
leikkauskuviona syntyvän ellipsin eksentrisyys (so. polttopisteiden etäisyys jaettuna ison
akselin pituudella) kaltevuuskulman
< 45o. Laske
leikkauskuviona syntyvän ellipsin eksentrisyys (so. polttopisteiden etäisyys jaettuna ison
akselin pituudella) kaltevuuskulman  funktiona.
funktiona.
Tehtävä 375
Onko edellisen tehtävän lasku pätevä, jos 45o < < 90o, ts. jos kyseessä on
hyperbelitapaus? Mikä on lausekkeen raja-arvo, kun
< 90o, ts. jos kyseessä on
hyperbelitapaus? Mikä on lausekkeen raja-arvo, kun 
 45o?
45o?
Tehtävä 376
Suoran ympyräkartion muodostajasuoran ja kartion pohjaympyrän välinen kulma on . Mikä on suurin eksentrisyyden arvo, mikä tason ja kartion leikkauskäyrällä
voi olla?
. Mikä on suurin eksentrisyyden arvo, mikä tason ja kartion leikkauskäyrällä
voi olla?
Tehtävä 377
Suoran ympyräkartion muodostajasuoran ja kartion pohjaympyrän välinen kulma on 60o . Kartiota leikataan tasolla, jonka kaltevuuskulma pohjaympyrään nähden on 30o, jolloin leikkauskäyrä on ellipsi. Laske Dandelinin pallojen säteet.9.3 Yhtälöt pääakselikoordinaatistossa
Tehtävä 378
Piirrä ellipsin 4x2 + 9y2 = 36 kuva käyttämällä parametriesitystä, jossa parametrina on eksentrinen anomalia.Tehtävä 379
Avaruudessa sijaitsevan ellipsin keskipiste on r0 (1, 2, 3) ja sen puoliakselit
määräytyvät vektoreista a = i + 2j - 3k, b = i + j + k. Mieti, miksi ellipsille voidaan
käyttää parametriesitystä r(t) = r0 + a cos t + b sin t. Laske tämän perusteella ellipsin
kehältä 100 pistettä. Piirrä ellipsin ortogonaaliprojektiot koordinaattitasoille.
(1, 2, 3) ja sen puoliakselit
määräytyvät vektoreista a = i + 2j - 3k, b = i + j + k. Mieti, miksi ellipsille voidaan
käyttää parametriesitystä r(t) = r0 + a cos t + b sin t. Laske tämän perusteella ellipsin
kehältä 100 pistettä. Piirrä ellipsin ortogonaaliprojektiot koordinaattitasoille.
Tehtävä 380
Johda sen ellipsin yhtälö, jonka polttoisteet ovat (0, 1) ja (0, -4) sekä eksentrisyys =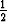 .
.
Tehtävä 381
Johda sen ellipsin yhtälö, jonka polttopisteet ovat (-1, 1) ja (3, 3) ja joka sivuaa x-akselia. Määritä ellipsin eksentrisyys.Tehtävä 382
Jana liikkuu siten, että sen toinen päätepiste liukuu x-akselia, toinen y-akselia pitkin. Johda sen käyrän yhtälö, jonka janalla oleva kiinteä piste piirtää. Mikä käyrä on kyseessä?Tehtävä 383
Pisteen O kautta kulkevien suorien s1 ja s2 välinen kulma olkoon . Pisteen
P etäisyys suorasta s1 olkoon d1 ja etäisyys suorasta s2 olkoon d2. Osoita, että ne pisteet
P , joille pätee d
. Pisteen
P etäisyys suorasta s1 olkoon d1 ja etäisyys suorasta s2 olkoon d2. Osoita, että ne pisteet
P , joille pätee d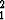 + d
+ d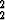 = 1, muodostavat ellipsin.
= 1, muodostavat ellipsin.
Tehtävä 384
Olkoot d1 ja d2 ellipsin polttopisteiden etäisyydet ellipsin tangentista. Osoita, että tulo d1d2 on vakio, so. tangentista riippumaton.Tehtävä 385
Olkoon tarkasteltavana kaksi O-keskistä ellipsiä, c1 ja c2:
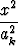 +
+ 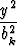 = 1, k = 1, 2.
= 1, k = 1, 2.
Olkoon piste P1 ellipsillä c1 ja olkoon s1 tähän pisteeseen asetettu ellipsin normaali;
vastaavasti P2 ja s2 ellipsin c2 suhteen. Mikä ehto täytyy lukujen a1, b1, a2 ja b2 täyttää,
jotta 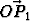 || s2
|| s2 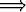
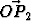 || s1?
|| s1?
Tehtävä 386
Johda sen hyperbelin yhtälö, jonka asymptootteina ovat suorat x ± 2y = 0 ja eräänä tangenttina suora x - y + 1 = 0.Tehtävä 387
Olkoon a > 0. Pisteet A (-a, 0) ja B
(-a, 0) ja B  (2a, 0) kärkinä on piirretty kolmio
ABP siten, että
(2a, 0) kärkinä on piirretty kolmio
ABP siten, että 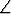 P AB =
P AB = 
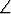 P BA. Minkä käyrän pisteet P muodostavat?
P BA. Minkä käyrän pisteet P muodostavat?
Tehtävä 388
Johda hyperbelille x2/a2 - y2/b2 = 1 parametriesitys
x = 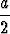 (t +
(t + 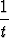 ), y =
), y = 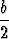 (t -
(t - 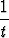 )
)
leikkaamalla käyrää laskevan asymptootin suuntaisilla suorilla.
Tehtävä 389
Osoita, että seuraava ellipsi ja hyperbeli ovat konfokaaliset, ts. niillä on yhteiset polttopisteet:
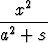 +
+ 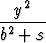 = 1,
= 1, 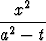 -
- 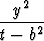 = 1, b2 < t < a2, s > -b2.
= 1, b2 < t < a2, s > -b2.
Näytä, että käyrät leikkaavat kohtisuorasti. Piirrä käyräparvien kuvaajia, kun parvien parametreina ovat s ja t.
Tehtävä 390
Todista, että hyperbelin asymptoottien ja tangentin rajoittaman kolmion ala on vakio.Tehtävä 391
Määritä ympyrä, joka kulkee paraabelin y2 = 2ax polttopisteen kautta ja sivuaa käyrää kahdessa pisteessä.Tehtävä 392
Johda sen paraabelin yhtälö, jonka polttopiste on (-1, 0) ja joka sivuaa y-akselia pisteessä (0, 2).Tehtävä 393
Johda sen paraabelin yhtälö, joka kulkee pisteiden (1, 0) ja (2, 0) kautta ja jolla on akselina suora y = x.Tehtävä 394
Johda niiden paraabelien yhtälöt, joiden akselina on suora x = 2y ja huippuna origo. Määritä näistä se, joka sivuaa suoraa y = 1.9.4 Yhtälöt napakoordinaateissa
Tehtävä 395
Millaista käyrää esittää napakoordinaattiyhtälö a) r(4 - 3 cos ) = 10,
b) r(3 - 4 cos
) = 10,
b) r(3 - 4 cos  ) = 10? Määritä eksentrisyys ja puoliakselit. Piirrä kuvio.
) = 10? Määritä eksentrisyys ja puoliakselit. Piirrä kuvio.
Tehtävä 396
Piirrä kuvat napakoordinaattikäyristä
r = 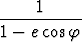 ,
,
kun e = 0, 0.25, 0.5, 0.75, 1, 1.25, 1.5. Mieti sopiva väli muuttujalle  . Mitä käyriä nämä
ovat?
. Mitä käyriä nämä
ovat?
Tehtävä 397
Määritä ellipsin r(1 - e cos ) = p keskipiste, polttopisteet ja puoliakselit.
Esitä käyrän yhtälö xy-koordinaatistossa.
) = p keskipiste, polttopisteet ja puoliakselit.
Esitä käyrän yhtälö xy-koordinaatistossa.
Tehtävä 398
Määritä hyperbelin r(±1 - e cos ) = p keskipiste, polttopisteet ja
puoliakselit. Esitä käyrän yhtälö xy-koordinaatistossa.
) = p keskipiste, polttopisteet ja
puoliakselit. Esitä käyrän yhtälö xy-koordinaatistossa.
Tehtävä 399
Ellipsin polttopisteet ovat (0, 0) ja (2, 2); sen ison akselin puolikas on a = 2. Määritä pikku akselin puolikas b ja eksentrisyys e sekä ellipsin yhtälö napakoordinaateissa. Piirrä kuvio.Tehtävä 400
Määritä käyrän a2(x + 1)2 + a2(y - 1)2 = (3x - y)2 laatu kaikilla parametrin a arvoilla.Tehtävä 401
Hyperbelin polttopisteeseen asetetun akselia vastaan kohtisuoran jänteen pituus on 4 ja hyperbelin eksentrisyys on 5. Määritä puoliakselien pituudet.Tehtävä 402
Kartioleikkaukseen piirretään samasta polttopisteestä kaksi vastakkaissuuntaista polttosädettä. Osoita, että niiden pituuksien käänteisarvojen summa on vakio.Tehtävä 403
Osoita, että jos paraabelille piirretään polttopisteestä neljä polttosädettä, joiden väliset kulmat ovat 90o, niin polttosäteiden pituuksien tulo saa pienimmän arvonsa 4p4 , kun paraabelin akseli puolittaa toisen polttosäteiden välisistä ristikulmapareista.Tehtävä 404
Ellipsin polttopisteet ovat (2, 2) ja (-2, 1) sekä johtosuora 4x + y = 14. Määritä ellipsin eksentrisyys ja johda yhtälö xy-koordinaatistossa.Tehtävä 405
Johda sen hyperbelin yhtälö, jonka toinen polttopiste on (1, 1) ja johtosuorat (kummallekin haaralle) x + y = ±1.9.5 Toisen asteen pintojen päätyypit
Tehtävä 406
Tutki, miten yksivaippaisen hyperboloidin x2 + y2 - z2 = 25 tangenttitaso 3x + 4y = 25 leikkaa pintaa.Tehtävä 407
Osoita, että yksivaippainen hyperboloidi x2 + y2 - z2 = 1 ja taso x + y - z = 1 leikkaavat toisensa pitkin kahta suoraa. Missä pisteessä nämä suorat leikkaavat toisensa? Mitkä ovat niiden suuntavektorit? Laske suorien välinen kulma.Tehtävä 408
Osoita laskemalla, että kartio
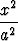 +
+ 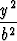 -
- 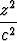 = 0
= 0
on hyperboloidien
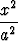 +
+ 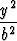 -
- 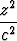 = ±1
= ±1
asymptoottikartio.
Tehtävä 409
Tutki, millainen on xy-tason ja hyperbolisen paraboloidin
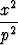 -
- 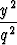 = 2z
= 2z
leikkauskäyrä.
Tehtävä 410
Koordinaatistoa kierretään 45o z-akselin ympäri. Millaisen muodon hyperbolisen paraboloidin x2 - y2 = 2z yhtälö tällöin saa?9.6 Yleinen toisen asteen käyrä
Tehtävä 411
Yhtälö xTAx + 2bTx + = 0, missä
= 0, missä
A = 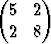 , b = -
, b = -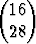 ,
,  = 80, x =
= 80, x = 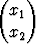 ,
,
esittää erästä x1x2-tason käyrää. Saata käyrän yhtälö muotoon f(x1, x2) = 0 ja piirrä käyrä. Miten matriisin A ominaisvektorit suhtautuvat käyrään?
Tehtävä 412
Olkoon
A = 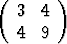 , b =
, b = 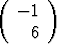 ,
,  = 12.
= 12.
Tutki toisen asteen käyrää xTAx + 2bTx +  = 0 ja osoita, että se on ellipsi. Määritä
eksentrisyys.
= 0 ja osoita, että se on ellipsi. Määritä
eksentrisyys.
Tehtävä 413
Tutki ja piirrä seuraavat toisen asteen käyrät:| a) | 5x2 + 5y2 + 6xy - 16x - 16y - 16 = 0, | ||
| b) | 8y2 + 6xy - 12x - 26y + 11 = 0, | ||
| c) | x2 - 2y2 + xy + x + 2y = 0, | ||
| d) | 4x2 + y2 - 4xy + 4x - 2y + 2 = 0. |
Tehtävä 414
Osoita, että seuraavat käyrät ovat paraabeleja:| a) | x2 + y2 + 2xy - 6x - 2y + 9 = 0, | ||
| b) | x2 + y2 - 2xy - 12x - 20y + 36 = 0, | ||
| c) | 16x2 + 9y2 + 24xy - 170x + 310y - 465 = 0. |
Määritä niiden akseli, huippu, huipputangentti, polttopiste ja johtosuora. Piirrä käyrät.
Tehtävä 415
Määritä a ja b siten, että yhtälö 2x2 + 2y2 + axy - 7x + by + 3 = 0 esittää kahta yhdensuuntaista suoraa.Tehtävä 416
Määritä käyrän x2 + y2 + 2axy + 2x + 2ay + b = 0 laatu kaikilla parametrien a ja b arvoilla.Tehtävä 417
Osoita, että kolmiparametrisen (parametreina a, d, k) käyräparven k2 x2 + y2 - 2kxy - 2(a2 + 1)(x + ky) + d = 0 kaikki käyrät ovat paraabeleja ja että niiden akselit kulkevat saman pisteen kautta.Tehtävä 418
Kolmiota rajoittavat suorat x = 0, y = mx, y = k(x - a). Laske kolmion korkeusjanojen leikkauspiste ja osoita, että se sijaitsee eräällä hyperbelillä, kun k muuttuu (ja m ja a ovat vakioita). Määritä hyperbelin keskipiste ja asymptootit. Piirrä kuvio.Tehtävä 419
Osoita, että jos käyrän xTAx + 2bTx + = 0 pisteessä P0
= 0 pisteessä P0  x0
toteutuu yhtälö Ax0 + b = o, niin käyrän yhtälö voidaan kirjoittaa muotoon
(x - x0 )T A(x - x0) = 0. Millainen käyrä ja millainen piste voi tulla kysymykseen?
x0
toteutuu yhtälö Ax0 + b = o, niin käyrän yhtälö voidaan kirjoittaa muotoon
(x - x0 )T A(x - x0) = 0. Millainen käyrä ja millainen piste voi tulla kysymykseen?
Tehtävä 420
Esittäköön yhtälö U(x) = xTAx + 2bTx + = 0 hyperbeliä, jonka keskipiste
on P0
= 0 hyperbeliä, jonka keskipiste
on P0  x0 . Osoita, että a) U(x) - U(x0) = 0 on asymptoottien yhteinen yhtälö,
b) U(x) - 2U(x0) = 0 on liittohyperbelin yhtälö, c) xTAx = 0 antaa origon kautta kulkevat
asymptoottien suuntaiset suorat.
x0 . Osoita, että a) U(x) - U(x0) = 0 on asymptoottien yhteinen yhtälö,
b) U(x) - 2U(x0) = 0 on liittohyperbelin yhtälö, c) xTAx = 0 antaa origon kautta kulkevat
asymptoottien suuntaiset suorat.
Tehtävä 421
Esittäköön yhtälö U(x) = xTAx + 2bTx + = 0 hyperbeliä; olkoon
= 0 hyperbeliä; olkoon
A = 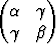 .
.
Osoita edellisen tehtävän perusteella, että hyperbelin asymptoottien kulmakertoimet
saadaan yhtälöstä  m2 + 2
m2 + 2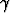 m +
m +  = 0. Laske tämän perusteella hyperbelin
2x2 - xy + 3x - y - 1 = 0 asymptootit.
= 0. Laske tämän perusteella hyperbelin
2x2 - xy + 3x - y - 1 = 0 asymptootit.
Tehtävä 422
Määritä pisteiden (0, -3), (-6, 0), (-4, 0) ja (0, -2) kautta kulkeva kartioleikkausparvi sekä tähän parveen kuuluvan paraabelin huippu.Tehtävä 423
Määritä kartioleikkausparvi, jonka käyrät kulkevat pisteiden (0, 1) ja (0, 3) kautta sekä sivuavat suoraa y = x pisteessä (1, 1). Määritä tähän parveen kuuluvan tasasivuisen hyperbelin keskipiste.Tehtävä 424
Määritä se kartioleikkaus, joka sivuaa ympyrää x2 + y2 = 2 pisteessä (1, 1), hyperbeliä 2x2 - 3y2 = 6 pisteessä (3, 2) ja kulkee pisteen (2, 2) kautta.Tehtävä 425
Määritä kaksiparametrinen kartioleikkausparvi, jonka käyrät kulkevat pisteiden (-1, 0) ja (1, 0) kautta sekä sivuavat suoraa x = 3.9.7 Yleinen toisen asteen pinta
Tehtävä 426
Kirjoita toisen asteen pinnan 3x2 + 3y2 + 3z2 - 4xy - 4yz - 4zx = 1 yhtälö matriisimuotoon. Laske matriisin ominaisarvot. Minkä tyyppinen pinta on kyseessä?Tehtävä 427
Tutki, millaista toisen asteen pintaa esittävät seuraavat yhtälöt:a) x2 - 2yz = 1, b) 3x2 + 15y2 - 5z2 - 12x - 10z + 22 = 0.
Tehtävä 428
Muodosta toisen asteen pintaa 2x2 + 6y2 + 2z2 + 8xz = 360 vastaava neliömatriisi ja määritä tämän ominaisarvot. Millainen pinta on kyseessä?Tehtävä 429
Tutki, millaista toisen asteen pintaa esittävät seuraavat yhtälöt:| a) | x2 + 2y2 - 3z2 + 12xy - 4yz - 8zx + 14x + 16y - 12z - 33 = 0, | ||
| b) | - xy + yz - zx + x + y + 2z - 2 = 0, | ||
| c) | 5x2 + y2 + z2 - 4xy - 2yz + 4zx + 2x + 1 = 0, | ||
| d) | y2 - z2 + 4xy - 4zx - 3 = 0, | ||
| e) | x2 - xy - yz + zx - 2x + y - z + 1 = 0, | ||
| f) | 36x2 + 9y2 + 4z2 + 36xy + 12yz + 24zx - 49 = 0. |
Tehtävä 430
Tutki, millaista toisen asteen pintaa esittävät seuraavat yhtälöt:| a) | 4x2 + 2y2 + 3z2 - 4yz + 4zx + 6x + 4y + 8z + 2 = 0, | ||
| b) | 4x2 + y2 + z2 + 4xy + 2yz + 4zx - 24x + 32 = 0. |
Tehtävä 431
Selosta, minkälaisia pintoja seuraavat toisen asteen yhtälöt esittävät:| a) | (x - 2)2 + (y - 3)2 = z2, | ||
| b) | (x + y)2 + (3x + 2y + z)2 = 0, | ||
| c) | (x + y)(3x + 2y + z) = 0, | ||
| d) | x2 + x - 5 = 0. |
Tehtävä 432
Määritä pinnan x2 + 2syz - t2 = 0 laatu kaikilla parametrien s ja t arvoilla.Tehtävä 433
Määritä a ja b siten, että yhtälö x2 - y2 + 3z2 + (ax + by)2 = 1 esittää pyörähdyslieriötä.Tehtävä 434
Osoita, että yhtälö 2xy + 2yz = 4zx esittää kartiopintaa. Määritä kartion akseli. Onko kyseessä pyörähdyspinta?Tehtävä 435
Kirjoita toisen asteen pinnan yleinen yhtälö. Osoita, että tämä on välttämättä muotoa axy + byz + czx = 0, jos suorakulmaisen avaruuskoordinaatiston x-, y- ja z-akseli sijaitsevat pinnalla. Millainen pinta on kyseessä, jos a) a = b = c = 2, b) a = 0, b = c = 2?Tehtävä 436
Todista, että neliparametrinen pintaparvi (parametreina a, b, c, d) x2 + az2 + 2yz + 2bzx + 2cx + 2dz + c2 = 0 sisältää korkeintaan kahta eri tyyppiä olevia pintoja. Mitkä tyypit tulevat kysymykseen?Tehtävä 437
Osoita, että jos pinnan xTAx + 2bTx + = 0 pisteessä P0
= 0 pisteessä P0  x0
toteutuu yhtälö Ax0 + b = o, niin pinnan yhtälö voidaan kirjoittaa muotoon
(x - x0 )T A(x - x0) = 0. Millainen pinta ja millainen piste voi tulla kysymykseen?
x0
toteutuu yhtälö Ax0 + b = o, niin pinnan yhtälö voidaan kirjoittaa muotoon
(x - x0 )T A(x - x0) = 0. Millainen pinta ja millainen piste voi tulla kysymykseen?
Tehtävä 438
Esittäköön yhtälö U(x) = xTAx + 2bTx + = 0 hyperboloidia, jonka
keskipiste on P0
= 0 hyperboloidia, jonka
keskipiste on P0  x0. Osoita, että a) U(x) - U(x0) = 0 on asymptoottikartion yhtälö ja
b) U(x) - 2U(x0) = 0 on liittohyperboloidin yhtälö.
x0. Osoita, että a) U(x) - U(x0) = 0 on asymptoottikartion yhtälö ja
b) U(x) - 2U(x0) = 0 on liittohyperboloidin yhtälö.
Tehtävä 439
Olkoon U(x) = xTAx + 2bTx + = 0 toisen asteen pinnan yhtälö. Osoita,
että muuttujan t toisen asteen yhtälöstä U(x0 +
= 0 toisen asteen pinnan yhtälö. Osoita,
että muuttujan t toisen asteen yhtälöstä U(x0 +  v) = 0 puuttuu ensimmäisen asteen
termi kaikilla vektoreilla v, jos ja vain jos Ax0 + b = o. Tulkitse tulos geometrisesti.
v) = 0 puuttuu ensimmäisen asteen
termi kaikilla vektoreilla v, jos ja vain jos Ax0 + b = o. Tulkitse tulos geometrisesti.
Tehtävä 440
Mitä voidaan sanoa toisen asteen pinnan xTAx + 2bTx + = 0 laadusta, jos
a) tiedetään, että matriisin A ominaisarvoista kaksi on erimerkkistä, mutta kolmannesta ei
tiedetä mitään; b) edellisen lisäksi tiedetään, että pintaa ei voida leikata tasoilla siten, että
leikkauskuvio olisi ellipsi; c) edellisten lisäksi tiedetään, että pinnalla on tasoleikkauksia,
joissa leikkauskuvio on paraabeli?
= 0 laadusta, jos
a) tiedetään, että matriisin A ominaisarvoista kaksi on erimerkkistä, mutta kolmannesta ei
tiedetä mitään; b) edellisen lisäksi tiedetään, että pintaa ei voida leikata tasoilla siten, että
leikkauskuvio olisi ellipsi; c) edellisten lisäksi tiedetään, että pinnalla on tasoleikkauksia,
joissa leikkauskuvio on paraabeli?
Tehtävä 441
Osoita, että jos toisen asteen pinnan yhtälössä x2 +
x2 +  y2 +
y2 + 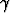 z2 + 2
z2 + 2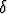 xy + 2
xy + 2 yz + 2
yz + 2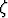 zx + 2
zx + 2 x + 2
x + 2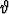 y + 2
y + 2 z +
z +  = 0 on
= 0 on  =
=  =
= 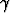 ja
ja 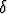 =
=  =
= 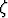 , niin kyseessä on pyörähdyspinta tai parabolinen lieriö. Mikä on
pyörähdyspinnan akselin suunta?
, niin kyseessä on pyörähdyspinta tai parabolinen lieriö. Mikä on
pyörähdyspinnan akselin suunta?
Tehtävä 442
Olkoon U pinta xTAx + 2bTx + = 0 ja U0 pinta xTAx = 0.
Osoita, että quad a) jos U on ellipsoidi tai piste, niin U0 on piste; b) jos U on
hyperboloidi tai kartio, niin U0 on kartio; c) jos U on elliptinen lieriö, elliptinen
paraboloidi tai suora, niin U0 on suora; d) jos U on hyperbolinen lieriö, hyperbolinen
paraboloidi tai kaksi leikkaavaa tasoa, niin U0 on kaksi leikkaavaa tasoa; e) jos U
on kaksi yhdensuuntaista tasoa, parabolinen lieriö tai taso, niin U0 on taso.
= 0 ja U0 pinta xTAx = 0.
Osoita, että quad a) jos U on ellipsoidi tai piste, niin U0 on piste; b) jos U on
hyperboloidi tai kartio, niin U0 on kartio; c) jos U on elliptinen lieriö, elliptinen
paraboloidi tai suora, niin U0 on suora; d) jos U on hyperbolinen lieriö, hyperbolinen
paraboloidi tai kaksi leikkaavaa tasoa, niin U0 on kaksi leikkaavaa tasoa; e) jos U
on kaksi yhdensuuntaista tasoa, parabolinen lieriö tai taso, niin U0 on taso.
Tehtävä 443
Tutki piirtämällä, mitä toisen asteen pintaa yhtälö 4x2 + 2y2 + 3z2 - 4yz + 4zx + 6x + 4y + 8z + 2 = 0 esittää. Määritä pinnan yhtälö pääakselikoordinaatistossa ja esitä tarvittava koordinaatistomuunnos. Mikä on uuden koordinaatiston origo ja mitkä ovat kantavektorit?Tehtävä 444
Tutki ominaisarvojen avulla, millaista toisen asteen pintaa esittää yhtälö36x2 + 9y2 + 4z2 + 36xy + 12yz + 24zx = 49.