10 Toisen asteen käyrien ja pintojen geometriaa
10.1 Ympyrän ja pallon ominaisuuksia
Tehtävä 446
Minkä käyrän muodostavat ne tason E2 pisteet, joista pisteitä (-a, 0) ja (a, 0) yhdistävä jana (a > 0) näkyy 45o kulmassa?Tehtävä 447
Osoita, että ne tason pisteet, joiden etäisyydet pisteistä P1 x1 ja P2
x1 ja P2  x2
ovat suhteessa k : 1, muodostavat Apolloniuksen ympyrän
x2
ovat suhteessa k : 1, muodostavat Apolloniuksen ympyrän
 2 =
2 = 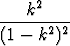
 2 (k
2 (k 1).
1).
Tehtävä 448
Määritä ympyrän ||x|| = 1 ja pisteen P0 x0 (tulkittuna ympyräksi, jonka
säde on = 0) kordaali.
x0 (tulkittuna ympyräksi, jonka
säde on = 0) kordaali.
Tehtävä 449
Olkoon c ympyrä K(x) = 0 ja olkoon P1 x1 sen ulkopuolella oleva piste.
Osoita, että yhtälö ||x - x1||2 = K(x1) esittää P1-keskistä ympyrää, joka leikkaa
ympyrän c kohtisuorasti. (Tätä kutsutaan ympyrän c ortogonaaliympyräksi.)
x1 sen ulkopuolella oleva piste.
Osoita, että yhtälö ||x - x1||2 = K(x1) esittää P1-keskistä ympyrää, joka leikkaa
ympyrän c kohtisuorasti. (Tätä kutsutaan ympyrän c ortogonaaliympyräksi.)
Tehtävä 450
Näytä, että ympyräparvet x2 + y2 - 2sy - c2 = 0 ja x2 + y2 - 2tx + c2 = 0 (parvien parametreina s ja t, c on vakio) leikkaavat toisensa kohtisuorasti. Piirrä kuvio.Tehtävä 451
Olkoon c ympyrä K(x) = 0 ja olkoon P1 x1 sen sisäpuolella oleva
piste. Osoita, että yhtälö ||x - x1||2 = -K(x1) esittää P1-keskistä ympyrää,
joka leikkaa ympyrän c halkaisijansa päätepisteissä. (Tätä kutsutaan ympyrän c
diametraaliympyräksi.)
x1 sen sisäpuolella oleva
piste. Osoita, että yhtälö ||x - x1||2 = -K(x1) esittää P1-keskistä ympyrää,
joka leikkaa ympyrän c halkaisijansa päätepisteissä. (Tätä kutsutaan ympyrän c
diametraaliympyräksi.)
Tehtävä 452
Olkoon c ympyrä, jonka säde on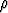 ja yhtälö K(x) = 0. Olkoon P1
ja yhtälö K(x) = 0. Olkoon P1  x1
sen sisäpuolella oleva piste. Muodosta yhtälö sille P1-keskiselle ympyrälle, joka
leikkaa ympyrän c sen halkaisijan päätepisteissä (ts. jonka diametraaliympyrä c
on).
x1
sen sisäpuolella oleva piste. Muodosta yhtälö sille P1-keskiselle ympyrälle, joka
leikkaa ympyrän c sen halkaisijan päätepisteissä (ts. jonka diametraaliympyrä c
on).
Tehtävä 453
Miten muodostetaan yksinkertaisimmin kahden annetun toisiaan leikkaavan ympyrän leikkauspisteiden kautta kulkeva ympyräparvi? Määritä se ympyröiden x2 + y2 - 6x + 4y - 12 = 0 ja x2 + y2 - 10x - 16y + 40 = 0 leikkauspisteiden kautta kulkeva ympyrä, jonka keskipiste on suoralla 8x - 3y - 2 = 0.Tehtävä 454
Näytä, että jos ympyröillä K1(x) = 0 ja K2(x) = 0 ei ole yhteisiä pisteitä, niin myöskään ympyröillä K1(x) + K2(x) = 0 ja K1(x) +
K2(x) = 0 ja K1(x) +  K2(x) = 0,
K2(x) = 0, 

 , ei ole
yhteisiä pisteitä.
, ei ole
yhteisiä pisteitä.
Tehtävä 455
Olkoon pallon yhtälö K(x) = 0 ja tason yhtälö L(x) = 0 (missä x = T). Miten muodostetaan pallon ja tason leikkausympyrän kautta
kulkevan palloparven yhtälö? Etsi sovellutuksena sen pallon yhtälö, joka kulkee pallon
K(x) = xT x - 1 = 0 ja tason L(x) = aTx = 0, missä a =
T). Miten muodostetaan pallon ja tason leikkausympyrän kautta
kulkevan palloparven yhtälö? Etsi sovellutuksena sen pallon yhtälö, joka kulkee pallon
K(x) = xT x - 1 = 0 ja tason L(x) = aTx = 0, missä a = 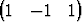 T, leikkausympyrän
kautta ja joka sivuaa tasoa x2 = 3.
T, leikkausympyrän
kautta ja joka sivuaa tasoa x2 = 3.
Tehtävä 456
Olkoon annettuna kolme palloa, joiden keskipisteet eivät ole samalla suoralla. Osoita, että pallojen kolme parittain otettua radikaalitasoa kulkevat saman suoran, ns. radikaaliakselin kautta. Osoita, että radiaakliakseli on kohtisuorassa pallojen keskipisteiden määräämää tasoa vastaan.Tehtävä 457
Olkoot K1(x) = 0 ja K2(x) = 0 kahden pallon yhtälöt. Osoita, että pallojen K1 (x) + K2 (x) = 0 ja K1(x) +
K2 (x) = 0 ja K1(x) +  K2(x) = 0,
K2(x) = 0, 
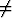 - 1,
- 1, 
 - 1,
- 1, 

 , radikaalitaso on
riippumaton lukujen
, radikaalitaso on
riippumaton lukujen  ,
,  valinnasta.
valinnasta.
Tehtävä 458
Osoita, että jokainen ympyrän x2 + y2 = a2, z = 0 kautta kulkeva pallo leikkaa ortogonaalisesti jokaisen pallon, joka kulkee ympyrän (x - b)2 + z2 = b2 - a2, y = 0 kautta.10.2 Liittohalkaisijat
Tehtävä 459
Ellipsiä 5x2 + 5y2 + 6xy - 16x - 16y = 16 leikataan suorilla, joiden suuntavektori on t1 = i + 2j. Osoita, että ellipsin näistä suorista erottamien jänteiden keskipisteet sijaitsevat samalla suoralla. Mikä on tämän suoran suuntavektori t2?Tehtävä 460
Totea, että edellisen tehtävän suuntavektorit toteuttavat ehdon t1TAt2 = 0, missä t1 ja t2 ovat suuntavektoreita vastaavat koordinaattivektorit ja A on ellipsin yhtälön toisen asteen termeistä saatava matriisi.Tehtävä 461
Suora x = x0 + v leikkaa toisen asteen käyrää xTAx + 2bTx +
v leikkaa toisen asteen käyrää xTAx + 2bTx +  = 0; tässä
A on symmetrinen 2 × 2 -matriisi, x, x0, v ja b kokoa 2 × 1 olevia pystyvektoreita sekä
= 0; tässä
A on symmetrinen 2 × 2 -matriisi, x, x0, v ja b kokoa 2 × 1 olevia pystyvektoreita sekä  ja
ja  skalaareja. Lausu leikkauspisteiden koordinaattivektorit suoraa ja käyrää
karakterisoivien vakioiden x0, v, A, b,
skalaareja. Lausu leikkauspisteiden koordinaattivektorit suoraa ja käyrää
karakterisoivien vakioiden x0, v, A, b,  avulla.
avulla.
Tehtävä 462
Todista, että ellipsin kahden liittohalkaisijan pituuksien neliöiden summa on vakio.Tehtävä 463
Määritä suoran a) e1T(Ax + b) = 0, b) e2T(Ax + b) = 0 liittohalkaisija toisen asteen käyrän xTAx + 2bTx + = 0 suhteen. (Tässä e1
= 0 suhteen. (Tässä e1  i, e2
i, e2  j ovat ortonormeeratut
kantavektorit.)
j ovat ortonormeeratut
kantavektorit.)
Tehtävä 464
Määritä pinnan2x2 + 5y2 + 11z2 - 20xy + 16yz + 4zx - 24x - 6y - 6z - 18 = 0
vektorin i - j suuntaisen halkaisijan liittohalkaisijatason yhtälö.
Tehtävä 465
Toisen asteen pinnan
 x2 +
x2 +  y2 +
y2 + 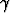 z2 + 2
z2 + 2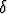 xy + 2
xy + 2 yz + 2
yz + 2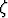 zx + 2
zx + 2 x + 2
x + 2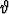 y + 2
y + 2 z +
z +  = 0
= 0
vektorin t suuntaisten jänteiden keskipisteet sijaitsevat xy-tason suuntaisessa tasossa. Määritä vektorin t suunta.
10.3 Polaariteoria
Tehtävä 466
Osoita, ettö kaksoissuhde on riippumaton suoran parametriesityksessä käytetyn suuntavektorin pituudesta.Tehtävä 467
Osoita laskemalla, että jos pisteistö P1, P2, P3, P4 on harmoninen, niin myös pisteistö P3 , P4, P1, P2 on.Tehtävä 468
Osoita, että avaruuden E3 pisteet P1 (1, 0, -1), P2
(1, 0, -1), P2  (3, -4, 5) ja
P3
(3, -4, 5) ja
P3  (8, -14, 20) ovat samalla suoralla. Määritä piste P4 siten, että pisteistö P1, P2, P3, P4
on harmoninen.
(8, -14, 20) ovat samalla suoralla. Määritä piste P4 siten, että pisteistö P1, P2, P3, P4
on harmoninen.
Tehtävä 469
Määritä suoran x + 2y = 3 napa a) käyrän 3x2 + y2 = 1, b) käyrän y = x2 suhteen. Piirrä kuvio.Tehtävä 470
Määritä käyrän 3x2 + 5y2 + 4xy - 7x - 8y - 3 = 0 tangentti ja normaali pisteessä (2, 1).Tehtävä 471
Millä ehdolla toisen asteen käyrä x2 +
x2 +  y2 + 2
y2 + 2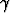 xy + 2
xy + 2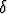 x + 2
x + 2 y +
y +  = 0
sivuaa x-akselia origossa?
= 0
sivuaa x-akselia origossa?
Tehtävä 472
Tarkastellaan toisen asteen käyrää x2 - xy - y = 0. a) Määritä tangenttijänteen avulla pisteestä (1, -2) käyrälle piirrettyjen tangenttien yhtälöt. b) Määritä suoran x + 2y + 3 = 0 suuntaisten käyrän tangenttien yhtälöt. Piirrä kuvio.Tehtävä 473
Olkoon s pisteen (2, 1) polaari ellipsin 5x2 + 5y2 + 6xy - 4x + 4y = 4 suhteen. Määritä ellipsille halkaisija, jonka liittohalkaisija on suoran s suuntainen.Tehtävä 474
Määritä käyrän x2 - 2y2 + 4xy - 6x + 2y = 0 origoon asetetun tangentin suuntaisten jänteiden liittohalkaisija. Piirrä kuvio.Tehtävä 475
Määritä suoran bTx + = 0 napa käyrän xTAx + 2bTx +
= 0 napa käyrän xTAx + 2bTx +  = 0
suhteen.
= 0
suhteen.
Tehtävä 476
Minkä käyrän muodostavat ympyrän xTx = 2 tangenttien navat ympyrän
xT x =
2 tangenttien navat ympyrän
xT x =  2 suhteen?
2 suhteen?
Tehtävä 477
Yhtälö (b1Tx + 1)(b2Tx +
1)(b2Tx +  2) = 0 esittää erästä toisen asteen käyrää.
Osoita, että tämän polaari pisteen P0
2) = 0 esittää erästä toisen asteen käyrää.
Osoita, että tämän polaari pisteen P0  x0 suhteen voidaan kirjoittaa
x0 suhteen voidaan kirjoittaa
(b1Tx0 +  1)(b2Tx +
1)(b2Tx +  2) + (b1Tx +
2) + (b1Tx +  1)(b2Tx0 +
1)(b2Tx0 +  2) = 0.
2) = 0.
Tutki, minkä tyyppinen toisen asteen käyrä voi olla kyseessä ja millaisia polaareja saadaan pisteen P0 sijainnista riippuen.
Tehtävä 478
Määritä tason ax + by + cz + d = 0 napa pinnan Ax2 + 2Byz + C = 0 suhteen.Tehtävä 479
Määritä ne pinnan z = xy pisteet, joihin asetetut normaalit muodostavat 45o kulman z-akselin kanssa.Tehtävä 480
Millä ehdolla toisen asteen pinta
 x2 +
x2 +  y2 +
y2 + 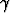 z2 + 2
z2 + 2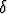 xy + 2
xy + 2 yz + 2
yz + 2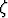 zx + 2
zx + 2 x + 2
x + 2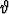 y + 2
y + 2 z +
z + 
sivuaa xy-tasoa origossa? Millä ehdolla origo on käyrän ja xy-tason ainoa yhteinen piste?
10.4 Viivoitin- ja pyörähdyspinnoista
Tehtävä 481
Johda sen pinnan yhtälö, joka muodostuu, kun hyperbeli x2 - 2z2 = 1, y = 0 pyörähtää suoran x = 0, y = 1 ympäri.Tehtävä 482
Johda sen kartion yhtälö, joka syntyy, kun x-akseli pyörähtää suoran x = y = z ympäri.Tehtävä 483
On annettuna kaksi suoraa: x = y, z = 0 ja x = y = z. Johda sen kartion yhtälö, joka syntyy, kun a) edellinen suora pyörähtää jälkimmäisen ympäri, b) jälkimmäinen pyörähtää edellisen ympäri.Tehtävä 484
Kartio, jonka kärki on pisteessä (0, 1, 1) leikkaa xy-tason pitkin paraabelia x= 2y. Määritä kartion ja xz-tason leikkauskäyrän eksentrisyys.Tehtävä 485
Johda sen kartion yhtälö, jonka kärki on origossa ja jonka vaippa kulkee yhtälöiden

määrittämän käyrän kautta.
Tehtävä 486
Ellipsin y2 + 4z2 = 4, x = 0 pisteet projisioidaan vektorin i - j + k suuntaisesti xz-tasolle. Määritä muodostuvan ellipsin puoliakselien pituudet.Tehtävä 487
Johda sen pyörähdyslieriön yhtälö, jolla on emäsuorana x = y = z ja jonka akseli kulkee pisteen (1, -1, -1) kautta.Tehtävä 488
Määritä sen elliptisen lieriön yhtälö, jonka vaippa sisältää ympyrät x2 + y2 = 1, z = 0 ja x2 + y2 - 4x + 2y + 4 = 0, z = 1.Tehtävä 489
Suoran x = t, y = t, z = 0 jokaisen pisteen kautta asetetaan vektorin i - j + tk suuntainen suora. Määritä syntyvän viivoitinpinnan yhtälö ja laatu.Tehtävä 490
Pinnalle z = xy asetetaan vektorin i + j + k suuntainen sivuava lieriö. Määritä sen ja xy-tason leikauskäyrä. Minkätyyppinen lieriö on kyseessä?Tehtävä 491
Määritä pitkin suoria
 ,
,  ja
ja 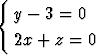
liukuvan suoran muodostama pinta.
Tehtävä 492
Pisteet P1 r1
r1  (1, 0, 1), P2
(1, 0, 1), P2  r2
r2  (0, 1, -1), P3
(0, 1, -1), P3  r3
r3  (-1, 0, 1),
P4
(-1, 0, 1),
P4  r4
r4  (0, -1, -1) muodostavat avaruusnelikulmion, so. nelikulmion, joka ei sijaitse
tasossa. Piste A kulkee suoraa P1P2 pitkin tasaisella nopeudella pisteestä P1 pisteeseen
P2 ja piste B samanaikaisesti suoraa P4P3 pitkin tasaisella nopeudella pisteestä P4
pisteeseen P3 . Etsi sen pinnan yhtälö, jonka suora AB liikkuessaan muodostaa.
(0, -1, -1) muodostavat avaruusnelikulmion, so. nelikulmion, joka ei sijaitse
tasossa. Piste A kulkee suoraa P1P2 pitkin tasaisella nopeudella pisteestä P1 pisteeseen
P2 ja piste B samanaikaisesti suoraa P4P3 pitkin tasaisella nopeudella pisteestä P4
pisteeseen P3 . Etsi sen pinnan yhtälö, jonka suora AB liikkuessaan muodostaa.
Tehtävä 493
Suora kulkee pisteen (1, 0, 0) kautta ja sen suuntavektori on j + k. Suora pyörähtää z-akselin ympäri, jolloin syntyy toisen asteen pinta. Määritä tämän yhtälö. Minkätyyppinen pinta on kyseessä?Tehtävä 494
Osoita, että suorat x = 1, y + z = 0 ja x = 1, y - z = 0 sijaitsevat kokonaisuudessaan edellisen tehtävän pinnalla. Leikkaavatko ne toisiaan?Tehtävä 495
Osoita, että emäsuoraparveen (parametrina s)
 , s
, s 
 .
.
kuuluvat kolme suoraa eivät ole saman tason suuntaisia.