12 Abstraktia algebraa
12.1 Ryhmä, rengas ja kunta
Tehtävä 502
Määritellään joukon A = {a, b, c} alkioiden laskutoimitus o seuraavalla taulukolla:| a | b | c | |||
| a | a | b | c | ||
| b | b | c | a | ||
| c | c | a | b |
Osoita, että (A, o) on Abelin ryhmä.
Tehtävä 503
Totea, että jos laskutoimituksena on kuvausten yhdistäminen, niin tason E2 tai avaruuden E3 translaatiot muodostavat Abelin ryhmän.Tehtävä 504
Tutki, muodostavatko a) tason E2, b) avaruuden E3 origokeskiset kierrot ryhmän, kun laskutoimituksena on kuvausten yhdistäminen. Onko kyseessä Abelin ryhmä?Tehtävä 505
Olkoon (A, +, o) kunta ja olkoot a, b A tunnettuja alkioita, a
A tunnettuja alkioita, a 0. Osoita,
että yhtälöllä aox = b on täsmälleen yksi ratkaisu x
0. Osoita,
että yhtälöllä aox = b on täsmälleen yksi ratkaisu x  A.
A.
Tehtävä 506
Totea esimerkiksi neliömatriiseja tarkastelemalla, että edellisen tehtävän yhtälöllä voi olla useita ratkaisuja tai ei ratkaisua lainkaan, jos (A, +, o) oletetaan vain renkaaksi.12.2 Lineaariavaruus
Tehtävä 507
Joukon 2 laskutoimitukset määritellään tavallisuudesta poikkeavalla
tavalla:
2 laskutoimitukset määritellään tavallisuudesta poikkeavalla
tavalla:
(x1 , y1) + (x2, y2) = (x1 + y2, x2 + y1),  (x, y) = (
(x, y) = ( x, y) (
x, y) (

 ).
).
Mitkä lineaariavaruuden aksioomat ovat tällöin voimassa?
Tehtävä 508
Avaruuden 2 osajoukossa E = { (x, y) | x + y = 2 } määritellään
laskutoimitukset seuraavasti:
2 osajoukossa E = { (x, y) | x + y = 2 } määritellään
laskutoimitukset seuraavasti:
| (x1, y1) + (x2, y2) = (x1 + x2 - 1, y1 + y2 - 1), | |||
 (x, y) = ( (x, y) = ( x + 1 - x + 1 -  , ,  y + 1 - y + 1 -  ) ( ) (   ). ). |
Osoita, että E on lineaariavaruus. Mikä on laskutoimitusten määrittelyn geometrinen sisältö?
Tehtävä 509
Ratkaise edellisen tehtävän joukossa E yhtälö (2, 0) + 7(x, y) = (-6, 8).Tehtävä 510
Olkoot a ja b reaalisen lineaariavaruuden E tunnettuja alkioita, olkoon x E tuntematon. Olkoon
E tuntematon. Olkoon 

 . Todista lineaariavaruuden aksioomiin perustuen, että
yhtälöllä
. Todista lineaariavaruuden aksioomiin perustuen, että
yhtälöllä  x + a = b on täsmälleen yksi ratkaisu. Mitä aksioomia tällöin tarvitaan?
x + a = b on täsmälleen yksi ratkaisu. Mitä aksioomia tällöin tarvitaan?
Tehtävä 511
Osoita, että enintään astetta n olevat polynomit muodostavat lineaariavaruuden. Muodostavatko täsmälleen astetta n olevat polynomit lineaariavaruuden?Tehtävä 512
Tutki, ovatko enintään toista astetta olevien polynomien muodostamaan lineaariavaruuteen kuuluvat polynomit p1(t) = 1 - t, p2(t) = t(1 - t), p3(t) = 1 - t2 lineaarisesti riippumattomia.Tehtävä 513
Osoita, että enintään astetta n olevien polynomien muodostaman lineaariavaruuden dimensio on n + 1.Tehtävä 514
Korkeintaan 1. astetta olevien reaalikertoimsten polynomien p(t) = at + b joukossa määritellään laskutoimitukset seuraavasti:| (p1 + p2)(t) = (a1 + a2) + (a1b2 + a2b1)t, | |||
( p)(t) = p)(t) =  bt. bt. |
Mitkä lineaariavaruuden aksioomat ovat voimassa?
12.3 Ekvivalenssirelaatio
Tehtävä 515
Luonnollisten lukujen p ja q välille määritellään relaatio R asettamalla
p R q 
 p on luvun q tekijä.
p on luvun q tekijä.
Tutki, onko relaatio a) refleksiivinen, b) symmetrinen, c) transitiivinen. Onko kyseessä ekvivalenssirelaatio?
Tehtävä 516
Tason suorien joukossa määritellään relaatio R asettamalla
s1 R s2 
 suorilla s1 ja s2 on yhteinen piste.
suorilla s1 ja s2 on yhteinen piste.
Tutki, onko relaatio a) refleksiivinen, b) symmetrinen, c) transitiivinen. Onko kyseessä ekvivalenssirelaatio?
Tehtävä 517
Joukon A relaatiota R sanotaan järjestysrelaatioksi, jos se on transitiivinen ja jos täsmälleen yksi ehdoista xRy, yRx ja x = y on voimassa mille tahansa alkioparille (x, y) A × A. Päättele, että relaatio < (x < y
A × A. Päättele, että relaatio < (x < y 
 x on pienempi kuin y) on
järjestysrelaatio joukossa
x on pienempi kuin y) on
järjestysrelaatio joukossa  .
.
Tehtävä 518
Olkoon P universumin U kaikkien osajoukkojen muodostama joukko. Tutki, ovatko joukko-opilliset osajoukkorelaatiot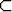 ja
ja 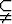 a) transitiivisia, b) järjestysrelaatioita
joukossa P.
a) transitiivisia, b) järjestysrelaatioita
joukossa P.
Tehtävä 519
Reaalilukuparien välille määritellään relaatio R seuraavasti:
(x1, y1) R (x2, y2) 
 x1 < x2
x1 < x2  y1 < y2.
y1 < y2.
Onko kyseesä järjestysrelaatio?