3 Lineaariset differentiaaliyhtälöt
3.1 Lineaariyhtälöiden teoriaa
Tehtävä 99
Onko differentiaaliyhtälö y'' + x(y' - y'') = y + 1 a) lineaarinen, b) homogeeninen?Tehtävä 100
Olkoot funktiot f(x) ja g(x) jatkuvasti derivoituvia välillä I ja olkoon tällä välillä f(x)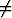 0. Etsi ensimmäisen kertaluvun lineaarinen differentiaaliyhtälö, jonka yleinen
ratkaisu on y = Cf(x) + g(x).
0. Etsi ensimmäisen kertaluvun lineaarinen differentiaaliyhtälö, jonka yleinen
ratkaisu on y = Cf(x) + g(x).
Tehtävä 101
Olkoon y1(x) = x2 ja y2(x) = x|x|. Osoita, että funktiot ovat lineaarisesti riippumattomia ja että niiden Wronskin determinantti on = 0. Onko mahdollista muodostaa toisen kertaluvun lineaarinen ja homogeeninen differentiaaliyhtälö, jonka ratkaisuja em. funktiot ovat?Tehtävä 102
Osoita, että eksponenttifunktio ja logaritmifunktio ovat differentiaaliyhtälön(x2 + x)y''' + (2 - x2)y'' - (2 + x)y' = 0
ratkaisuja. Mikä on yhtälön yleinen ratkaisu?
Tehtävä 103
Osoita, että differentiaaliyhtälölläx(3 + x)y''' + (12 - x2)y'' - 3(4 + x)y' = 0
on ratkaisuina y = ex ja y = 1/x2. Mikä on differentiaaliyhtälön yleinen ratkaisu?
Tehtävä 104
Osoita, että eksponenttifunktio ja logaritmifunktio ovat differentiaaliyhtälöä(x2 + x)y''' + (2 - x2)y'' - (2 + x)y' = 2(1 - x - x2)
vastaavan homogeeniyhtälön ratkaisuja. Totea, että epähomogeenisella yhtälöllä on ratkaisuna eräs toisen asteen polynomi. Mikä on yhtälön yleinen ratkaisu?
Tehtävä 105
Määritä laskentaohjelmalla Besselin differentiaaliyhtälön x2 y'' + xy' + (x2 - n2)y = 0 yleinen ratkaisu. Tässä n on parametri, joka voi saada minkä tahansa reaaliarvon. Kokeile ensin symbolilla n, ja anna sille tämän jälkeen kokonaislukuarvoja ja yksinkertaisia murtolukuarvoja. Ratkaisut ovat muotoa C1 y1 (x) + C2 y2(x). Miten funktiot y1 ja y2 suhtautuvat toisiinsa parametrin n eri arvoilla? Millaisia ominaisuuksia niillä on? Rajoitu tarkastelemaan arvoja x > 0.Tehtävä 106
Tutki, millaisia kohdassa x = 0 annettuja alkuehtoja arvoa n = 1 vastaavaan Besselin differentiaaliyhtälöön x2y'' + xy' + (x2 - 1)y = 0 voidaan liittää. Mikä on tilanne, jos ehdot annetaan kohdassa x = 1?Tehtävä 107
Muodosta toisen kertaluvun homogeeninen lineaarinen differentiaaliyhtälö, jolla on yksityisratkaisuina kahdesti derivoituvat funktiot y1(x) ja y2(x), joiden Wronskin determinantti on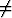 0.
0.
Tehtävä 108
Lineaarisella homogeenisella toisen kertaluvun differentiaaliyhtälöllä on yksityisratkaisuina y1(x) = x ja y2(x) = cos x. Muodosta yhtälö ja määritä sen ratkaisuista se, jonka kuvaaja sivuaa suoraa y = x + 1 origossa.Tehtävä 109
Olkoon funktio P (x) derivoituva. Tee differentiaaliyhtälöön y'' + P (x)y' + Q(x)y = 0 sijoitus
y(x) = u(x)e-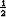
 P(x) dx
P(x) dx
ja saata se muotoon u'' + I(x)u = 0. Millainen funktio on I(x)?
Tehtävä 110
Olkoon funktio P (x) jatkuva. Kerro differentiaaliyhtälö y'' + P (x)y' + Q(x)y = 0 funktiolla
p(x) = e P(x) dx
P(x) dx
ja saata tulos muotoon
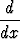
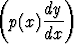 + q(x)y = 0.
+ q(x)y = 0.
Millainen funktio on q(x)?
Tehtävä 111
Olkoon y1(x) yhtälön
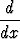
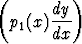 + q1(x)y = 0
+ q1(x)y = 0
ei-triviaali (/ 0) ratkaisu ja y2(x) yhtälön
0) ratkaisu ja y2(x) yhtälön
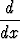
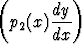 + q2(x)y = 0
+ q2(x)y = 0
nollasta eroava (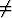 0
0 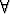 x) ratkaisu. Todista Piconen identtisyys
x) ratkaisu. Todista Piconen identtisyys
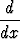
![[ ]
y1(p1y'y2- p2y1y')
y2 1 2](kuvat/dy167x.gif) = (q2 - q1)y
= (q2 - q1)y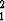 + (p1 - p2)y1'2 + p2
+ (p1 - p2)y1'2 + p2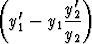 2.
2.
Tehtävä 112
Nesteeseen upotettu massa m on ripustettu pystysuoraan kierrejouseen, jonka jousivakio on k. Massa saatetaan pystysuoraan värähdysliikkeeseen antamalla sille alkupoikkeama ja alkunopeus; lisäksi siihen vaikuttaa ajan mukana muuttuva pystysuora ulkoinen voima F (t). Neste vastustaa liikettä nopeuteen verrannollisella voimalla (verrannollisuuskerroin = c). Johda systeemiä kuvaava differentiaaliyhtälö.Tehtävä 113
Tutki edellisen tehtävän differentiaaliyhtälöä numeerisesti. Aseta ulkoinen voima jaksolliseksi: F (t) = F0 cos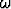 t. Valitse yhtälössä oleviksi vakioiksi esimerkiksi
m = 1, k = 5, c = 2, F0 = 1,
t. Valitse yhtälössä oleviksi vakioiksi esimerkiksi
m = 1, k = 5, c = 2, F0 = 1, 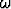 = 1. Tutki systeemin käyttäytymistä ajan funktiona. Mitä
mahdetaan tarkoittaa ratkaisun transientilla komponentilla ja tasapainotilaratkaisulla
(steady state solution)?
= 1. Tutki systeemin käyttäytymistä ajan funktiona. Mitä
mahdetaan tarkoittaa ratkaisun transientilla komponentilla ja tasapainotilaratkaisulla
(steady state solution)?
Tehtävä 114
Muuta edellisen tehtävän systeemin parametreja siten, että se kuvaa tilannetta, missä neste ei vastusta liikettä. Etsi joko kokeellisesti tai laskemalla sellainen voiman F (t) taajuus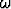 , että systeemi on resonanssissa; tällöin heilahtelun
amplitudi kasvaa rajatta. Miten systeemi käyttäytyy em. resonanssikohdan lähellä?
, että systeemi on resonanssissa; tällöin heilahtelun
amplitudi kasvaa rajatta. Miten systeemi käyttäytyy em. resonanssikohdan lähellä?
Tehtävä 115
Tutki, voidaanko edellisen tehtävän mukaiseen rajatta kasvavaan amplitudiin (ja siis systeemin rikki räjähtämiseen) joutua, jos neste vastustaa liikettä.3.2 Homogeenisen yhtälön ratkaiseminen
Tehtävä 116
Yhtälölläy' + P (x)y = (x + 1)2ex
on ratkaisuna y = (x2 - 1)ex. Määritä P (x) ja yhtälön yleinen ratkaisu. Etsi alkuehdon y(0) = 5 toteuttava yksityisratkaisu.
Tehtävä 117
Funktiot y1(x) ja y2(x) ovat yhtälön y' + a(x)y = 0 ratkaisuja, vastaavasti y1 (x) + ex ja y2(x) - 1 yhtälön y' + a(x)y + b(x) = 0 ratkaisuja. Määritä se jälkimmäisen yhtälön ratkaisu, jonka kuvaaja kulkee origon kautta.Tehtävä 118
Määritä seuraavien yhtälöiden yleiset ratkaisut, kun eräs yksityisratkaisu tai sen muoto on annettu:| a) xy'' - (x + 3)y' + y = 0, polynomi, | |||
| b) x2(ln x - 1)y'' - xy' + y = 0, polynomi, | |||
| c) (x2 - 2x - 1)y'' - 2(x - 1)y' + 2y = 0, polynomi, | |||
| d) y'' + (tan x - 2 cot x)y' + 2(cot 2x)y = 0, sin x, | |||
| e) y'' + 2(1 - tan 2x)y = 0, cos 2x, | |||
| f) (x - 2)y'' - (4x - 7)y' + (4x - 6)y = 0, ekx. |
Tehtävä 119
Mikä yksinkertainen alkeisfunktio on differentiaaliyhtälön y'' + P (x)y' + Q(x)y = 0 ratkaisuna, jos 1 + P (x) + Q(x) 0? Ratkaise tämän nojalla
yhtälöt
0? Ratkaise tämän nojalla
yhtälöt
| a) (x - 1)y'' - xy' + y = 0, | |||
| b) (2x - x2)y'' + (x2 - 2)y' + (2 - 2x)y = 0, | |||
c) y'' - 2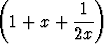 y' + y' + 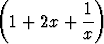 y = 0. y = 0. |
Tehtävä 120
Etsi jollakin symbolisella ohjelmalla Airyn differentiaaliyhtälön y'' - xy = 0 yleinen ratkaisu. Etsi yksityisratkaisut, kun alkuehtona on a) y(0) = 0, y'(0) = 1, b) y(0) = 1, y' (0) = 0. Piirrä ratkaisujen kuvaajat samaan kuvioon. Tarkastele erityisesti negatiivisia muuttujan arvoja. Miten ratkaisufunktioiden nollakohdat näyttävät suhtautuvan toisiinsa?3.3 Täydellisen yhtälön ratkaiseminen
Tehtävä 121
Ratkaise yhtälöta) y' + 2xy = 2xe-x2 , b) (1 + x2)y' - 2xy = (1 + x2)2, c) y' sin x - y = 1 - cos x.
Tehtävä 122
Ratkaise seuraavat alkuarvoprobleemat:| a) xy' + 2y = x3, y(1) = 1, | |||
| b) y' + y cos x = sin x cos x, y(0) = 1, | |||
c) y' + 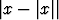 y = x, y(0) = 0. y = x, y(0) = 0. |
Tehtävä 123
Ratkaise alkuarvoprobleema
y' + y cot x = ecos x, y(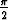 ) = 1.
) = 1.
Piirrä ratkaisukäyrä.
Tehtävä 124
Määritä se kaikilla muuttujan x arvoilla jatkuva funktio y(x), joka toteuttaa integraaliyhtälön
2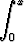 ty(t) dt = x2 + y(x).
ty(t) dt = x2 + y(x).
Tehtävä 125
Funktio q(x) olkoon kaikilla arvoilla x jatkuva ja toteuttakoon epäyhtälön q(x) < x2 . Olkoon y(x) yhtälön y' + 3x2y = q(x) ratkaisu, joka toteuttaa alkuehdon y(0) = 0. Mitä arvoja y(-1) voi saada?Tehtävä 126
Etsi ne käyrät, joilla x-akselin, käyrän pisteeseen osoittavan paikkavektorin ja tähän pisteeseen asetetun tangentin muodostaman kolmion ala on = a (vakio).Tehtävä 127
Differentiaaliyhtälöllä y'' + y = 0 on yksityisratkaisuina sin x ja cos x. Etsi yleisellä vakioiden varioinnilla differentiaaliyhtälöidena) y'' + y = tan x, b) y'' + y = 2x sin x
yleiset ratkaisut.
Tehtävä 128
Ratkaise alkuarvoprobleema y'' + x(y' - y'') = y + 1, y(0) = y'(0) = 0.Tehtävä 129
Etsi differentiaaliyhtälön y'' + y' tan x = x tan x yleinen ratkaisu.Tehtävä 130
Etsi differentiaaliyhtälön (x - 1)y'' - xy' + y = x - 1 yleinen ratkaisu.Tehtävä 131
Totea, että differentiaaliyhtälöä (x + 1)y'' - xy' - y = (x + 1)2 vastaavan homogeeniyhtälön lineaarisesti riippumattomiksi ratkaisuiksi kelpaavat
y1(x) = ex, y2(x) = ex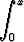
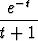 dt.
dt.
Etsi em. epähomogeenisen differentiaaliyhtälön yleinen ratkaisu ja alkuehdon y(0) = y' (0) = 0 toteuttava yksityisratkaisu.
Tehtävä 132
Olkoon h(x) lineaarista vakiokertoimista differentiaaliyhtälöä y'' + py' + qy = R(x) vastaavan homogeeniyhtälön ratkaisu, joka toteuttaa alkuehdot h(0) = 0, h' (0) = 1. Osoita, että
y(x) = 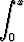 h(x - t)R(t) dt
h(x - t)R(t) dt
on epähomogeenisen yhtälön yksityisratkaisu, jolle y(0) = y'(0) = 0. Ratkaise tällä menettelyllä alkuarvoprobleema y'' + y = tan x, y(0) = y'(0) = 0.
Tehtävä 133
Bernoulli’n differentiaaliyhtälö on muotoa y' = A(x)y + B(x)yk. Se voidaan palauttaa lineaariseksi ensimmäisen kertaluvun yhtälöksi sijoituksella z = y1-k. Ratkaise tällä tavoin seuraavat Bernoulli’n yhtälöt:| a) xy' + y = x3y2, | b) y' + y = y2(cos x - sin x), | ||||||
| c) 3y' + y = (1 - 2x)y4, | d) y' + 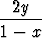 = 4(x2 - x) = 4(x2 - x)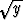 . . |
Tehtävä 134
Riccati’n differentiaaliyhtälö on muotoa y' = A(x) + B(x)y + C(x)y2. Jos sen yksityisratkaisu y0(x) tunnetaan, se voidaan palauttaa Bernoulli’n yhtälöksi sijoituksella y = y0 + z. Ratkaise tällä tavoin seuraavat Riccati’n yhtälöt, joiden yksityisratkaisun muoto tunnetaan:| a) y' = 1 + x + x2 - (2x + 1)y + y2, y0(x) = ax + b, | |||
| b) y' = y2 - x2y - (x - 1)2, y0(x) = ax2 + bx + c, | |||
c) x2y' + (xy - 2)2 = 0, y0(x) = 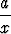 . . |
3.4 Vakiokertoimiset yhtälöt
Tehtävä 135
Etsi seuraavien yhtälöiden yleiset ratkaisut:a) y' - y = cosh x, b) y' - y = ex - sin x.
Tehtävä 136
Ratkaise alkuarvoprobleemat| a) y' + 2y = x3 - x, y(1) = 1, | b) y' + 3y = x3 + 1, y(1) = 2, | ||||||
| c) y' + y = sinh x, y(0) = 0. |
Tehtävä 137
Osoita, että sillä yhtälön y' = x + |y| ratkaisulla, joka toteuttaa alkuehdon y(-2) = 1, on minimi y(ln 2 - 1) = ln 2 - 1.Tehtävä 138
Määritä yhtälön y' = |y - x| yleinen ratkaisu. Piirrä suuntakenttä ja ratkaisukäyriä. Määritä y(1), kun y toteuttaa alkuehdon a) y(-1) = -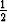 , b) y(-1) =
, b) y(-1) = 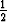 .
.
Tehtävä 139
Olkoon a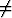 0. Yhtälön y' + ay = A sin
0. Yhtälön y' + ay = A sin 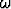 x ratkaisuista vain yksi on
jaksollinen. Määritä tämän amplitudi.
x ratkaisuista vain yksi on
jaksollinen. Määritä tämän amplitudi.
Tehtävä 140
Etsi seuraavien yhtälöiden yleiset ratkaisut:| a) y'' + 4y' + 5y = 3x - 2, | b) y'' - y' - 2y = 4x, | c) y'' - 7y' + 6y = sin x, | |||||||||
| d) y'' + 4y = sin 3x, | e) y'' + 2y' + 5y = e-x, | f) y'' - 2y' + y = ex + cos x, | |||||||||
| g) y'' + 4y' + 4y = e-2x + sin x, | h) y'' - 4y = xe2x, | i) y'' - 6y' + 9y = e3x/x2. |
Tehtävä 141
Ratkaise alkuarvotehtävä:y'' - 2y' + y = sin x, y(0) = y'(0) = 1.
Tehtävä 142
Ratkaise seuraavat alku- tai reuna-arvoprobleemat:| a) y'' - 4y' + 5y = sin x, y(0) = 0, y'(0) = -1, | |||
| b) y'' - 3y' + x2 - 1 = 0, y(0) = 1, y'(0) = 0, | |||
| c) y'' - 5y' + 6y = ex, y(0) = y(1) = 0. |
Tehtävä 143
Ratkaise alkuarvoprobleema y'' + 5y' + 6y = x, y(0) = 1, y'(0) = 0.Tehtävä 144
Ratkaise alkuarvoprobleema
y'' + y = 2 sin x, y(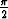 ) = 1, y'(
) = 1, y'(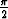 ) =
) = 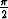 .
.
Tehtävä 145
Ratkaise kaikilla a, b

| a) y'' + ay' = ebx, | b) y'' - a2y = ebx, | c) y'' + a2y = ebx, | |||||||||
| d) y'' + a2y = sin bx, | e) y'' + a2y = x sin bx, | f) y'' + 2y' + (1 + a2)y = ebx. |
Tehtävä 146
Sovella yleistä vakioiden variointia yhtälön y'' + ay' + by = R(x) yksityisratkaisun etsimiseen, kun a2 - 4b on a) > 0, b) = 0, c) < 0.Tehtävä 147
Ratkaise differentiaaliyhtälö y'' +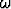 2y = A sin
2y = A sin 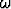 x + B cos
x + B cos 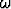 x.
x.
Tehtävä 148
Pidetään tunnettuna, että homogeeniyhtälön y'' +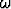 2y = 0 ratkaisut
ovat y1 (x) = sin
2y = 0 ratkaisut
ovat y1 (x) = sin 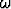 x, y2(x) = cos
x, y2(x) = cos 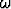 x. Sovella vakioiden variointia yhtälön
y'' +
x. Sovella vakioiden variointia yhtälön
y'' + 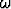 2 y = A sin
2 y = A sin 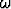 x + B cos
x + B cos 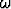 x yksityisratkaisun etsimiseen.
x yksityisratkaisun etsimiseen.
Tehtävä 149
Laske yhtälön y'' + ay' + by = 0 perusratkaisujen Wronskin determinantti vakioiden a, b kaikilla arvoilla.Tehtävä 150
Määritä ne reaaliset parametrin a arvot, joilla yhtälöilläy'' + 2ay' - 4y = 0 ja y'' - 2y' + ay = 0
on yhteinen ei-triviaali (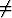
 0) ratkaisu. Ratkaise yhtälöt näillä parametrin
arvoilla.
0) ratkaisu. Ratkaise yhtälöt näillä parametrin
arvoilla.
Tehtävä 151
Ratkaise yhtälöy''' - 2y'' - y' + 2y = e4x.
Tehtävä 152
Ratkaise differentiaaliyhtälö:y''' - 3y'' + 7y' - 5y = ex.
Tehtävä 153
Ratkaise differentiaaliyhtälöt| a) y(5) + 2y''' + y' = 0, | b) y(7) + 3y(6) + 3y(5) + y(4) = 0, | ||||||
| c) y''' + 3y'' - 2y = sin x, | d) y(4) + 3y''' + 3y'' + y' = 2e-2x - 2x. |
Tehtävä 154
Ratkaise differentiaaliyhtälöy'''' - 4y''' + 12y'' + 4y' - 13y = 9e2x + 52x - 3.
Tehtävä 155
Ratkaise differentiaaliyhtälö y'''' + 3y''' + 3y'' + y' = 2e-2x - 2x.Tehtävä 156
Ratkaise alkuarvoprobleemat| a) y''' - 5y'' + 17y' - 13y = 0, y(0) = y'(0) = y''(0) = 1, | |||
| b) y''' - ky' = 0, y(0) = 0, y'(0) = 1, y''(0) = 2, | |||
| c) y''' - y'' - y' + y = e2x, y(0) = y'(0) = y''(0) = 0. |
Tehtävä 157
Ratkaise alkuarvoprobleema y''' - 2y'' - y' + 2y = 2x2 - 6x + 4, y(0) = 5, y' (0) = -5, y''(0) = 1.Tehtävä 158
Etsi kaikki differentiaaliyhtälön y''' + y'' + 2y' + 2y = 0 jaksolliset ratkaisut.Tehtävä 159
Ratkaise kaikilla arvoilla a
 differentiaaliyhtälöt
differentiaaliyhtälöt
a) y(4) + a4y = x2, b) y''' - (a + 2)y'' + (2a + 1)y' - ay = x + 1.
Tehtävä 160
Muunna Eulerin differentiaaliyhtälöx2y'' + axy' + by = 0
sijoituksella t = ln |x| vakiokertoimiseksi lineaariyhtälöksi. Sovella tulosta yhtälöön
x2y'' - xy' + y = 0,
ratkaise saatu vakiokertoiminen yhtälö ja muodosta tämän avulla alkuperäisen yhtälön yleinen ratkaisu.
Tehtävä 161
Ratkaise differentiaaliyhtälö x2y'' + 3xy' + y = 0 kokeilemalla muotoa y = xr olevaa yritettä.Tehtävä 162
Etsi differentiaaliyhtälön x2y'' + 5xy' + y = 0 yleinen ratkaisu muotoa y = xr olevaa yritettä käyttäen. Etsi alkuehtoa y(1) = 1, y'(1) = 2 vastaava yksityisratkaisu.Tehtävä 163
Ratkaise differentiaaliyhtälö x2y'' - 2xy' + 2y = x2 sin x yritteellä y = xr sekä yleisellä vakioiden varioinnilla. Kirjoita yhtälöt, joista saadaan integroimisvakioiden arvot, kun alkuehtona on y(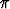 ) = 1, y'(
) = 1, y'(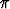 ) = 0.
) = 0.
Tehtävä 164
Etsi yleinen ratkaisu differentiaaliyhtälölle x2y'' + xy' - y = 4.Tehtävä 165
Etsi seuraavien differentiaaliyhtälöiden yleiset ratkaisut:| a) x2 y'' - xy' + y = 0, | b) x2y'' - 9xy' + 21y = 0, | c) x2y'' - 2xy' + 2y = x, | |||||||||
| d) x2 y'' + xy' - y = x2, | e) x2y'' + xy' + y = x3 - 2x, | f) x2y'' - 4xy' + 6y = 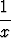 . . |
Tehtävä 166
Ratkaise kaikilla p, q
 differentiaaliyhtälö
differentiaaliyhtälö
x2y'' + (2p + 1)xy' + qy = 0.
Tehtävä 167
Ratkaise differentiaaliyhtälöta) (x + 1)2 y'' + (x + 1)y' + y = x2, b) (3x + 2)2y'' + 7(3x + 2)y' + 63x - 18 = 0.
Tehtävä 168
Ratkaise alkuarvoprobleemax3y''' + xy' - y = 0, y(1) = 1, y'(1) = 2, y''(1) = 3.
Tehtävä 169
Ratkaise kaikilla arvoilla a
 differentiaaliyhtälö x3y''' + 2ax2y'' - 4a(xy' - y) = 0.
differentiaaliyhtälö x3y''' + 2ax2y'' - 4a(xy' - y) = 0.
Tehtävä 170
Ratkaise seuraava differentiaaliyhtälö valitsemalla apumuuttujaksi y' /x:x2y''' + 2(x2 - x)y'' + (x2 - 2x + 2)y' = x3.
Tehtävä 171
Etsi integro-differentiaaliyhtälön
x2y'(x) + 2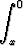 y(t) dt = 0
y(t) dt = 0
kaikki ratkaisut johtamalla ensin differentiaaliyhtälö funktiolle y.
Tehtävä 172
Sähköisen RL-piirin differentiaaliyhtälö on
L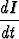 + RI = E(t),
+ RI = E(t),
missä tuntematin funktio I(t) esittää virtaa, L ja R (induktanssi ja vastus) ovat piirille
karakteristisia vakioita ja E(t) on piiriin syötetty jännite. Ratkaise differentiaaliyhtälö
tapauksissa a) E(t) = E0 = vakio, b) E(t) = E0 sin 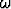 t. Millainen fysikaalinen tulkinta
ratkaisulle voidaan antaa?
t. Millainen fysikaalinen tulkinta
ratkaisulle voidaan antaa?
Tehtävä 173
Olkoot R, L, E ja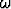 positiivisia vakioita, I(t) tuntematon funktio. Etsi
differentiaaliyhtälölle
positiivisia vakioita, I(t) tuntematon funktio. Etsi
differentiaaliyhtälölle
L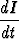 + RI = E sin
+ RI = E sin 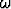 t
t
jaksollinen ratkaisu. Mikä on tätä ratkaisua vastaava alkuehto origossa? Mikä on jakson pituus?
Tehtävä 174
Pitkin x-akselia liikkuvan massapisteen yhtälö olkoon
m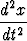 = -kx,
= -kx,
missä muuttuja t on aika, massa m ja k positiivisia vakioita. Määritä x(t) alkuehdolla x(0) = R, x' (0) = 0. Miten pitkän ajan kuluttua massapiste palaa lähtökohtaansa, jos R = 6.36 . 106 m ja x''(0) = -9.8 m/s2? Mikä on probleeman fysikaalinen sisältö?
Tehtävä 175
Ratkaise yhtälö x''(t) + x'(t) + g = 0, missä
x'(t) + g = 0, missä  ja g ovat positiivisia vakioita.
Sovella alkuehtoa x(0) = 0, x'(0) = v0 ja määritä se muuttujan t arvo, jolla x'(t) = 0.
Mikä on probleeman fysikaalinen sisältö?
ja g ovat positiivisia vakioita.
Sovella alkuehtoa x(0) = 0, x'(0) = v0 ja määritä se muuttujan t arvo, jolla x'(t) = 0.
Mikä on probleeman fysikaalinen sisältö?