1 Lukujonot ja vakiotermiset sarjat
1.1 Lukujono
Tehtävä 1
Todista, että lukujono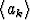 suppenee ja sen raja-arvo on < 2, kun jono
määritellään rekursiivisesti
suppenee ja sen raja-arvo on < 2, kun jono
määritellään rekursiivisesti
a0 = 0, ak+1 = 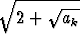 , k = 0, 1, 2, . . . .
, k = 0, 1, 2, . . . .
Esitä yhtälö, josta raja-arvo voidaan ratkaista.
Tehtävä 2
Lukujono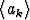 määritellään rekursiivisesti
määritellään rekursiivisesti
a1 = 1, ak+1 = 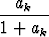 , k = 1, 2, 3, . . . .
, k = 1, 2, 3, . . . .
Määritä limk ak.
Tehtävä 3
Olkoon
fk(x) = 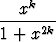 , x
, x 
 , k
, k 
 .
.
Määritä limk
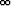 fk(x) kaikilla x
fk(x) kaikilla x 
 . Piirrä funktioiden fk kuvaajia. Millainen on
raja-arvofunktion kuvaaja?
. Piirrä funktioiden fk kuvaajia. Millainen on
raja-arvofunktion kuvaaja?
Tehtävä 4
Tutki, suppenevatko seuraavat kompleksiset lukujonot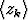 :
:
a) zk = 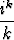 , b) zk =
, b) zk = 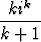 , c) zk =
, c) zk = 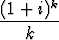 .
.
Tehtävä 5
Tutki, suppenevatko seuraavat kompleksitason lukujonot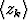 :
:
a) zk = 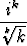 , b) zk =
, b) zk = 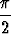 +
+ 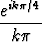 , c) zk =
, c) zk = 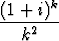 .
.
Onko jonoilla kasautumispisteitä? Piirrä jonojen pisteitä kompleksitasoon.
Tehtävä 6
Olkoon sk yksikköympyrän sisään piirretyn säännöllisen 2k-kulmion sivun pituus. Johda rekursiokaava, jossa sk+1 lausutaan edellisen luvun sk avulla. Mikä on sopiva alkuarvo täten saatavalle rekursiivisesti määritellylle jonolle?Tehtävä 7
Muodosta edellisen tehtävän jonon avulla lukujono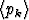 , missä jonon luvut
esittävät yksikköympyrän sisään piirretyn 2k-kulmion piiriä. Laske tämän jonon termejä ja
yritä saada näiden avulla niin tarkka approksimaatio luvulle
, missä jonon luvut
esittävät yksikköympyrän sisään piirretyn 2k-kulmion piiriä. Laske tämän jonon termejä ja
yritä saada näiden avulla niin tarkka approksimaatio luvulle  kuin mahdollista. Kuinka
monta oikeata desimaalia saadaan?
kuin mahdollista. Kuinka
monta oikeata desimaalia saadaan?
Tehtävä 8
Lukujono muodostetaan rekursiokaavalla xn+1 = 1 - ax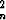 , missä x0 = 0.
Parametrille a pätee 0 < a < 2. Tutki kokeellisesti, miten jono käyttäytyy suurilla indeksin
n arvoilla: laske 100 – 200 jonon lukua ja tulosta sen jälkeen näkyviin 10 – 20 seuraavaa
lukua. Tarkastele erityisesti parametriarvoja a = 0.5, 0.8, 1, 1.3, 1.39, 1.6.
, missä x0 = 0.
Parametrille a pätee 0 < a < 2. Tutki kokeellisesti, miten jono käyttäytyy suurilla indeksin
n arvoilla: laske 100 – 200 jonon lukua ja tulosta sen jälkeen näkyviin 10 – 20 seuraavaa
lukua. Tarkastele erityisesti parametriarvoja a = 0.5, 0.8, 1, 1.3, 1.39, 1.6.
Tehtävä 9
Onko edellisen tehtävän jonolla raja-arvoa? Lausu raja-arvo parametrin a funktiona ja piirrä funktion kuvaaja. Mitä mahdetaan tarkoittaa käsitteillä yläraja-arvo ja alaraja-arvo (lim sup, lim inf, limes superior, limes inferior)? Entä lukujonon kasautumispisteellä?1.2 Vakioterminen sarja
Tehtävä 10
Laske sarjan

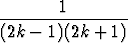
osasummia pienillä indeksin arvoilla ja arvaa näiden perusteella osasumman sn lauseke. Todista arvauksesi. Osoita, että sarja suppenee ja määritä sen summa.
Tehtävä 11
Laske sarjan

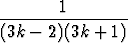
osasummia pienillä indeksin arvoilla ja arvaa näiden perusteella osasumman sn lauseke. Todista arvauksesi. Osoita, että sarja suppenee ja määritä sen summa.
Tehtävä 12
Laske sarjan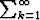 1/k2 osasummia, ja tutki, miten lähelle sarjan summaa
päästään. Tarkka arvo on
1/k2 osasummia, ja tutki, miten lähelle sarjan summaa
päästään. Tarkka arvo on  2/6. Tutki samalla tavoin sarjaa
2/6. Tutki samalla tavoin sarjaa

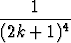 ,
,
jonka summa on  4/96.
4/96.
Tehtävä 13
Todista, että suppenevan sarjan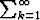 ak termien joukko { ak | k
ak termien joukko { ak | k 
 } on
rajoitettu.
} on
rajoitettu.
Tehtävä 14
a) Olkoon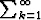 ak suppeneva sarja. Todista, että jokaisella p
ak suppeneva sarja. Todista, että jokaisella p 
 myös sarja
myös sarja
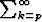 ak suppenee. b) Olkoon
ak suppenee. b) Olkoon 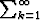 ak hajaantuva sarja. Todista, että jokaisella p
ak hajaantuva sarja. Todista, että jokaisella p 
 myös
sarja
myös
sarja 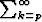 ak hajaantuu.
ak hajaantuu.
Tehtävä 15
a) Todista, että jos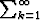 ak suppenee ja
ak suppenee ja 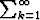 bk hajaantuu, niin
bk hajaantuu, niin
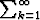 (ak + bk ) hajaantuu. b) Näytä esimerkillä, että jos
(ak + bk ) hajaantuu. b) Näytä esimerkillä, että jos 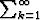 ak ja
ak ja 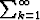 bk hajaantuvat,
niin
bk hajaantuvat,
niin 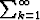 (ak + bk) voi olla suppeneva sarja.
(ak + bk) voi olla suppeneva sarja.
Tehtävä 16
Olkoon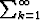 ak suppeneva sarja ja sen summa = s. Osoita, että sarja
ak suppeneva sarja ja sen summa = s. Osoita, että sarja
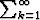 (ak + ak+2) suppenee, ja määritä sen summa.
(ak + ak+2) suppenee, ja määritä sen summa.
Tehtävä 17
Osoita oikeaksi tai vääräksi seuraavat väitteet: a) Jos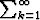 ak suppenee, niin
myös
ak suppenee, niin
myös 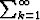 (ak + a
(ak + a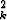 ) suppenee. b) Jos
) suppenee. b) Jos 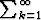 a
a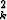 suppenee, niin myös
suppenee, niin myös 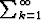 (ak + a
(ak + a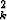 )
suppenee.
)
suppenee.
Tehtävä 18
Todista: Jos sarja |ak| suppenee, niin myös sarja
|ak| suppenee, niin myös sarja  ak suppenee. Päteekö
käänteinen lause?
ak suppenee. Päteekö
käänteinen lause?
Tehtävä 19
Olkoot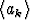 ja
ja 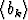 kaksi lukujonoa, joille pätee ak = bk+1 - bk,
k = 1, 2, 3, . . . . Osoita, että sarja
kaksi lukujonoa, joille pätee ak = bk+1 - bk,
k = 1, 2, 3, . . . . Osoita, että sarja  ak suppenee, jos ja vain jos jono
ak suppenee, jos ja vain jos jono 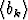 suppenee.
suppenee.