2 Sarjojen suppenemiskriteerejä
2.1 Geometrinen sarja
Tehtävä 20
Tutki, millä arvoilla x
 sarja
sarja
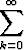
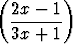 k
k
suppenee. Määritä summafunktio ja piirrä sen kuvaaja.
Tehtävä 21
Millä muuttujan x
 arvoilla sarja
arvoilla sarja
 tan kx
tan kx
suppenee? Mikä on sen summa? Piirrä summafunktion kuvaaja.
Tehtävä 22
Tutki, millä arvoilla x
 sarja
sarja
 2k cos 2x sin 2kx
2k cos 2x sin 2kx
suppenee. Määritä summafunktio ja piirrä sen kuvaaja.
Tehtävä 23
Millä reaalisilla muuttujan x arvoilla sarja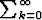 e-kx suppenee? Mikä on
tällöin sen summa?
e-kx suppenee? Mikä on
tällöin sen summa?
Tehtävä 24
Määritä sarjan

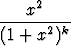
summa. Onko summafunktio jatkuva?
Tehtävä 25
Kehitä funktio
f(x) = 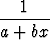 , a
, a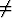 0, b
0, b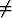 0,
0,
sarjaksi a) muuttujan x nousevien, b) sen laskevien potenssien mukaan. Millä muuttujan arvoilla sarja suppenee?
Tehtävä 26
Akhilles ja kilpikonna juoksevat kilpaa. Akhilles juoksee kymmenen kertaa niin nopeasti kuin kilpikonna. Varmana voitostaan Akhilles antaa kilpikonnalle yhden stadionin (164 – 192 metriä muinaiskreikkalaisesta paikkakunnasta riippuen) etumatkan. Kun Akhilles on juossut yhden stadionin, on kilpikonna juossut stadionin kymmenesosan ja on siis tämän verran edellä. Kun Akhilles on juossut tämän kymmenesosan verran lisää, on kilpikonna juossut yhden sadasosastadionin lisää ja on edelleen edellä. Näin kilpailu jatkuu loppumattomiin kilpikonnan jatkuvasti johtaessa. Eikö Akhilles voitakaan? Jos voittaa, niin miten pitkän matkan juostuaan hän ohittaa kilpikonnan?2.2 Positiivitermiset sarjat
Tehtävä 27
Tutki seuraavien sarjojen suppenemista annettuja positiivitermisten sarjojen suppenemistestejä käyttäen:a) 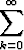 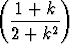 2, 2, | vertailutesti, | ||||||
b) 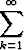 k2 sin k2 sin 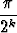 , , | suhdetesti, | ||||||
c) 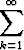 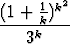 , , | juuritesti, | ||||||
d)  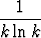 , , | integraalitesti. |
Tehtävä 28
Olkoon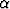 > 0. Tutki integraalitestiä käyttäen, suppeneeko sarja
> 0. Tutki integraalitestiä käyttäen, suppeneeko sarja

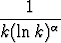 .
.
Perustele myös, miksi integraalitestiä voidaan käyttää. Miten sarja käyttäytyy, jos
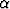 < 0?
< 0?
Tehtävä 29
Tutki vertailutestien avulla seuraavien sarjojen suppenemista:
a) 
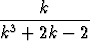 , b)
, b) 
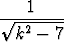 , c)
, c)  (
(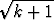 -
- 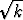 ).
).
Tehtävä 30
Olkoon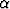 > 0. Muodosta sopiva vertailusarja, jolla voidaan tutkia
sarjan
> 0. Muodosta sopiva vertailusarja, jolla voidaan tutkia
sarjan

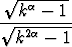
suppenemista. Millä parametrin 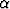 arvoilla sarja suppenee, millä hajaantuu?
arvoilla sarja suppenee, millä hajaantuu?
Tehtävä 31
Olkoon p, q
 , 0 < q < p. Tutki seuraavien sarjojen suppenemista:
, 0 < q < p. Tutki seuraavien sarjojen suppenemista:
a) 
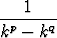 , b)
, b) 
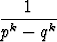 , c)
, c) 
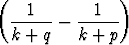 .
.
Tehtävä 32
Tutki seuraavien sarjojen suppenemista:
a) 
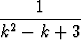 , b)
, b) 
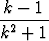 , c)
, c) 
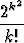 .
.
Tehtävä 33
Tutki seuraavien sarjojen suppenemista:
a) 
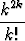 , b)
, b) 
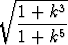 , c)
, c)  (pk)-
(pk)- , p
, p 
 .
.
Tehtävä 34
Tutki seuraavien sarjojen suppenemista:
a) 
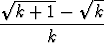 , b)
, b) 
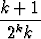 , c)
, c) 
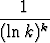 .
.
Tehtävä 35
Tutki seuraavien sarjojen suppenemista:
a) 
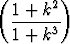 k, b)
k, b) 
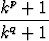 , p, q
, p, q 
 , c)
, c) 
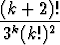 .
.
Tehtävä 36
Tutki seuraavien sarjojen suppenemista:
a) 
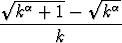 ,
, 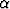 > 0, b)
> 0, b) 
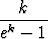 , c)
, c) 
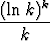 .
.
Tehtävä 37
Olkoon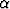

 . Tutki seuraavien sarjojen suppenemista:
. Tutki seuraavien sarjojen suppenemista:
a) 
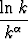 , b)
, b) 
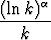 , c)
, c) 
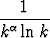 .
.
Tehtävä 38
Olkoon
ak = 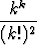 .
.
Osoita, että limk
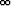 ak = 0 tarkastelemalla sarjaa
ak = 0 tarkastelemalla sarjaa  ak.
ak.
Tehtävä 39
Todista: Jos a1 > a2 > . . . > ak > ak+1 > . . . > 0 ja sarja ak suppenee,
niin limk
ak suppenee,
niin limk
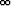 kak = 0.
kak = 0.
Tehtävä 40
Osoita esimerkillä, että jos edellisessä tehtävässä luovutaan jonoa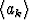 koskevasta monotonisuusoletuksesta, niin väite ei enää välttämättä päde.
koskevasta monotonisuusoletuksesta, niin väite ei enää välttämättä päde.
2.3 Vuorottelevat sarjat
Tehtävä 41
Osoita, että sarja

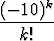
suppenee. Määritä sarjan summa yhden tuhannesosan tarkkuudella.
Tehtävä 42
Tutki seuraavien sarjojen suppenemista:
a) 
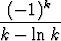 , b)
, b) 
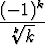 , c)
, c) 
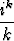 .
.
Tehtävä 43
Tutki seuraavien sarjojen suppenemista:
a)  (-1)k
(-1)k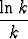 , b)
, b) 
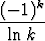 , c)
, c)  (-1)k(
(-1)k(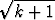 -
- 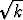 ).
).
Tehtävä 44
Arvioi, montako termiä on otettava sarjasta

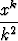 ,
,
jotta sen summalle pisteessä x = - saataisiin likiarvo, jonka virhe on < 10-4?
saataisiin likiarvo, jonka virhe on < 10-4?
Tehtävä 45
Luku voidaan laskea seuraavista sarjoista:
voidaan laskea seuraavista sarjoista:
 =
= 
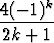 =
= 
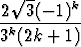 .
.
Kuinka monta termiä sarjoihin on otettava, jotta  saataisiin 10 desimaalin
tarkkuudella?
saataisiin 10 desimaalin
tarkkuudella?
Tehtävä 46
Tarkastellaan sarjaa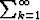 ak, missä
ak, missä
a2p-1 = 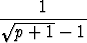 , a2p = -
, a2p = -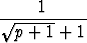 , p = 1, 2, 3, . . . .
, p = 1, 2, 3, . . . .
Kirjoita sarjan kahdeksan ensimmäistä termiä. Osoita, että sarja hajaantuu ryhmittämällä termit kahden termin ryhmiin (ts. laske a2p-1 + a2p). Miksi sarjaan ei voida soveltaa Leibnizin lausetta?
Tehtävä 47
Olkoon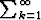 ak suppeneva positiiviterminen sarja. Osoita, että tällöin
myös sarja
ak suppeneva positiiviterminen sarja. Osoita, että tällöin
myös sarja 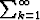 a
a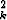 suppenee. Päteekö väite yleisesti, jos luovutaan lukujen ak
positiivisuudesta?
suppenee. Päteekö väite yleisesti, jos luovutaan lukujen ak
positiivisuudesta?
Tehtävä 48
Laske jonkin symbolisen tietokoneohjelman avulla harmonisten sarjojen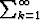 1/kp summia. Millaisia tuloksia saadaan luvun p eri arvoilla? Entä jos käytetään
eksponenttina symbolia p? (Tuloksissa esiintyy ns. Riemannin
1/kp summia. Millaisia tuloksia saadaan luvun p eri arvoilla? Entä jos käytetään
eksponenttina symbolia p? (Tuloksissa esiintyy ns. Riemannin 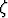 -funktion arvoja. Tällä
funktiolla on tiettyä kuuluisuutta mm. siihen liittyvien avoimien matemaattisten
ongelmien vuoksi.)
-funktion arvoja. Tällä
funktiolla on tiettyä kuuluisuutta mm. siihen liittyvien avoimien matemaattisten
ongelmien vuoksi.)