3 Itseisesti suppenevat sarjat
3.1 Itseinen suppeneminen
Tehtävä 49
Tutki suhdetestin avulla, suppeneeko sarja
.
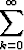
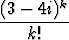Tehtävä 50
Olkoon ak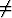
- 1 kaikilla indekseillä k. Osoita, että jos sarja 
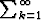ak suppenee
itseisesti, niin myös sarja
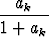
suppenee itseisesti.
Tehtävä 51
Millä arvoilla x
sarja
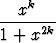
suppenee?
Tehtävä 52
Millä arvoilla x sarja
xk tan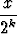 
suppenee?
Tehtävä 53
Todista, että sarja
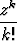
suppenee kaikilla z 
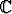osoittamalla sarja ensin itseisesti suppenevaksi. Sijoita sarjaan
z = i
ja laske sarjan osasummia numeerisesti. Mikä on sarjan summa tällä
muuttujan arvolla? Mikä tunnettu kompleksimuuttujan funktio mahtaa olla sarjan
summafunktio?
3.2 Sarjan termien uudelleen järjestäminen
Tehtävä 54
Osoita, että sarja
(-1)k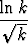
suppenee, mutta ei suppene itseisesti. Sarjan termit järjestetään uudelleen siten, että sen summaksi tulee 3. Laske sarjan summa tarkkuutena 0.1. Montako sarjan termiä tähän tarvitaan?
Tehtävä 55
Esitä jokin tapa järjestää sarjan
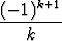
termit siten, että sarja hajaantuu.
3.3 Cauchyn tulo
Tehtävä 56
Osoita, että sarja
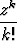
suppenee ja suppenee itseisesti kaikilla z 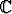. Summafunktio olkoon E(z). Osoita
Cauchyn tuloa käyttäen, että E(z1)E(z2) = E(z1 + z2). Mikä funktio E(z) itse asiassa
on?
Tehtävä 57
Muodosta sarjojen
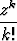ja 
bk
Cauchyn tulo ja vaadi, että tämä on = 1 (so. sarja, jonka nollas termi on = 1 ja muut termit = 0). Määritä termit bk. Mitä funktioita sarjat mahtavat esittää?
Tehtävä 58
Laske numeerisesti sarjan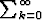
(-1)k/
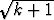osasummien jonon 30
ensimmäistä termiä. Piirrä tämän jonon kuvaaja. Suppeneeko sarja? Muodosta sarjan
Cauchyn tulo itsensä kanssa ja laske tämän osasummien jonosta 30 ensimmäistä termiä.
Piirrä kuvaaja. Näyttääkö sarja suppenevan?
Tehtävä 59
Olkoon
ak =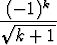 
.
Muodosta sarjan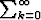 
ak Cauchyn tulo itsensä kanssa. Totea, että alkuperäinen sarja
suppenee, mutta ei itseisesti, ja että sen Cauchyn tulo hajaantuu. Jälkimmäistä varten
todista ensin epäyhtälö
(j + 1)(k - j + 1) < (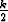
+ 1)2
ja sovella sitä Cauchyn tulon termin arvioimiseen.