4 Funktiojonot ja funktiotermiset sarjat
4.1 Funktiojono ja funktioterminen sarja
Tehtävä 60
Tutki, millä muuttujan x
 arvoilla funktiojono
arvoilla funktiojono  suppenee,
kun
suppenee,
kun
a) fk(x) =  , b) fk(x) =
, b) fk(x) =  , c) fk(x) =
, c) fk(x) =  .
.
Mikä on rajafunktio?
Tehtävä 61
Tutki, millä muuttujan x
 arvoilla sarja
arvoilla sarja  fk suppenee, kun
fk suppenee, kun
a) fk(x) = 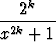 , b) fk(x) =
, b) fk(x) =  , c) fk(x) =
, c) fk(x) =  .
.
Piirrä summafunktion kuvaaja.
4.2 Pisteittäinen ja tasainen suppeneminen
Tehtävä 62
Määritä funktiojonon
fn(x) = 
rajafunktio joukossa  . Piirrä funktioiden fn kuvaajia. Onko suppeneminen
tasaista?
. Piirrä funktioiden fn kuvaajia. Onko suppeneminen
tasaista?
Tehtävä 63
Tarkastellaan reaalilukujoukossa funktiojonoja
fn(x) = 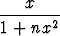 ja gn(x) = f'n(x).
ja gn(x) = f'n(x).
Piirrä funktioiden kuvaajia. Tutki, suppenevatko funktiojonot tasaisesti. Millaisia ovat rajafunktiot?
Tehtävä 64
Tarkastellaan reaalilukujoukossa funktiojonoja
fn(x) =  ja gn(x) = f'n(x).
ja gn(x) = f'n(x).
Piirrä funktioiden kuvaajia. Tutki, suppenevatko funktiojonot tasaisesti. Millaisia ovat rajafunktiot?
Tehtävä 65
Olkoon
f(x) = nx(1 - x)n, x  [0, 1].
[0, 1].
Määritä rajafunktio f(x) = limn
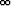 fn(x) ja tutki, onko suppeneminen tasaista. Piirrä
funktioiden kuvaajia.
fn(x) ja tutki, onko suppeneminen tasaista. Piirrä
funktioiden kuvaajia.
Tehtävä 66
Olkoon
fn(x) = limp
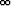 (cos n!
(cos n! x)2p, x
x)2p, x 
 , p
, p 
 .
.
Suppeneeko funktiojono  kaikilla x
kaikilla x 
 ? Minkälainen on rajafunktio? Tarkastele
erikseen muuttujan x rationaali- ja irrationaaliarvoja.
? Minkälainen on rajafunktio? Tarkastele
erikseen muuttujan x rationaali- ja irrationaaliarvoja.
Tehtävä 67
Osoita, että sarja

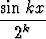
suppenee tasaisesti joukossa  . Piirrä summafunktion kuvaaja.
. Piirrä summafunktion kuvaaja.
Tehtävä 68
Osoita Weierstrassin testiä käyttäen, että sarja


suppenee tasaisesti joukossa  .
.
Tehtävä 69
Osoita, että sarja
 (-1)k
(-1)k
suppenee tasaisesti jokaisella rajoitetulla välillä [-a, a]. Voidaanko tarkastelussa käyttää Weierstrassin testiä? Entä Leibnizin lausetta?
Tehtävä 70
Tutki, suppeneeko sarja


tasaisesti välillä [0,  [. Onko suppeneminen tasaista välillä [a,
[. Onko suppeneminen tasaista välillä [a,  [, missä a > 0?
[, missä a > 0?
Tehtävä 71
Osoita Weierstrassin testiä käyttäen, että funktioterminen sarja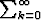
 suppenee tasaisesti kompleksitason ympyrärenkaassa 2 < |z| < 3.
suppenee tasaisesti kompleksitason ympyrärenkaassa 2 < |z| < 3.
Tehtävä 72
Osoita, että sarja


suppenee tasaisesti kaikilla x 
 . Laske sarjan summa pisteissä x = 0,
. Laske sarjan summa pisteissä x = 0,  ,
,  .
.
Tehtävä 73
Tutki, suppeneeko sarja

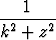
tasaisesti siinä kompleksitason joukossa, joka saadaan poistamalla termien nimittäjien nollakohdat ympyrästä |z| < R (R vakio).
Tehtävä 74
Oletetaan, että sarja fk(x) suppenee tasaisesti ja
fk(x) suppenee tasaisesti ja  |fk(x)| pisteittäin
välillä [a, b]. Seuraako tästä, että
|fk(x)| pisteittäin
välillä [a, b]. Seuraako tästä, että  |fk(x)| suppenee tasaisesti ko. välillä? Tarkastele
esimerkkinä funktioita fk(x) = (-1)kxk(1 - x) välillä [0, 1].
|fk(x)| suppenee tasaisesti ko. välillä? Tarkastele
esimerkkinä funktioita fk(x) = (-1)kxk(1 - x) välillä [0, 1].
4.3 Tasainen suppeneminen ja jatkuvuus
Tehtävä 75
Tutki, millä muuttujan x
 arvoilla sarja
arvoilla sarja

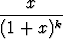
suppenee ja määritä sen summa. Piirrä summafunktion kuvaaja. Onko summafunktio määrittelyalueessaan jatkuva? Suppeneeko sarja tasaisesti välillä [0, 1]? Entä välillä [1, 2]? Perustele vastauksesi.
Tehtävä 76
Osoita, että sarja


suppenee tasaisesti koko reaalilukujoukossa. Onko sarjan summafunktio jatkuva? Piirrä tämän kuvaaja.
4.4 Termeittäin derivointi ja integrointi
Tehtävä 77
Funktiojono määritellään seuraavasti:
määritellään seuraavasti:
fn(x) = ![2 1
{ n x, kun x (- [0,n],
- n2x + 2n, kun x (- [1, 2],
n n
0 muulloin.](kuvat/sa238x.gif)
Määritä jonon rajafunktio. Päteekö
limn
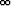
 fn(x) dx =
fn(x) dx =  limn
limn
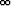 fn(x) dx ?
fn(x) dx ?
Tehtävä 78
Olkoon g : [0, 1]
 jatkuva funktio ja olkoon
jatkuva funktio ja olkoon 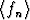 edellisen tehtävän
funktiojono. Määritä
edellisen tehtävän
funktiojono. Määritä
limn
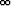
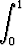 fn(x)g(x) dx.
fn(x)g(x) dx.
Tehtävä 79
Laske sarjojen
 e-kx ja
e-kx ja  ke-kx
ke-kx
summafunktiot. Millä muuttujan arvoilla sarjat suppenevat?
Tehtävä 80
Laske sarjan


summa laskemalla ensin integraali  xk-1 dx. Perustele laskusi.
xk-1 dx. Perustele laskusi.
Tehtävä 81
Osoita, että sarja
s(x) =  ke-kx
ke-kx
suppenee tasaisesti välillä [1, 2] ja laske integraali  s(x) dx.
s(x) dx.
Tehtävä 82
Osoita, että sarja

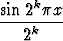
suppenee tasaisesti kaikilla x 
 . Voidaanko sarja derivoida termeittäin? Piirrä
alkuperäisen sarjan ja termeittäin derivoimalla saadun sarjan osasummien kuvaajia.
. Voidaanko sarja derivoida termeittäin? Piirrä
alkuperäisen sarjan ja termeittäin derivoimalla saadun sarjan osasummien kuvaajia.
Tehtävä 83
Tutki, millä arvoilla x
 funktio
funktio
s(x) =  ekx/k2
ekx/k2
on määritelty. Millä alueella summafunktion derivaatta ja integraalifunktio voidaan muodostaa termeittäin derivoimalla ja integroimalla?