5 Potenssisarjat
5.1 Määritelmä ja suppeneminen
Tehtävä 84
Määritä seuraavien potenssisarjojen suppenemisympyrät:
a) 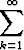
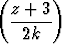 k, b)
k, b) 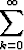
![[ ]
-----z----
2 + (- 1)k](kuvat/sa256x.gif) k, c)
k, c) 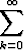
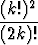 (z - i)k.
(z - i)k.
Tehtävä 85
Määritä seuraavien potenssisarjojen suppenemisympyrät:
a) 
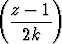 k, b)
k, b) 
![[z - 1- i]
------k--
2 + i](kuvat/sa262x.gif) k, c)
k, c) 
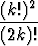 z2k.
z2k.
Tehtävä 86
Määritä seuraavien potenssisarjojen suppenemisympyrät:
a) 
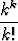 (z - 1)k, b)
(z - 1)k, b) 
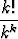 (z - i)k, c)
(z - i)k, c)  kp(z + 2 + 3i)k, p
kp(z + 2 + 3i)k, p 
 .
.
Tehtävä 87
Määritä potenssisarjan

 k
k
suppenemissäde. Piirrä summafunktion kuvaaja.
Tehtävä 88
Määritä potenssisarjan
 (-1)k
(-1)k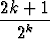 z2k
z2k
suppenemissäde ja summa palauttamalla se sopivaan geometriseen sarjaan.
Tehtävä 89
Laske sarjan
 (-1)kkx2k-1
(-1)kkx2k-1
summa tulkitsemalla se erään toisen sarjan derivaataksi. Mikä on sarjan suppenemissäde?
Tehtävä 90
Osoita, että sarja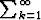 k/3k suppenee ja määritä sen summa.
k/3k suppenee ja määritä sen summa.
Tehtävä 91
Funktio f määritellään potenssisarjan summana
f(z) = 
![1
---------kk-
[2 + (- 1) ]](kuvat/sa277x.gif) zk
zk
suppenemisympyrässä. Piirrä funktion kuvaaja, kun muuttuja z rajoitetaan reaaliseksi.
Tehtävä 92
Potenssisarjan
 ckzk
ckzk
kertoimet toteuttavat rekursion
c1 = 1, ck+1 = 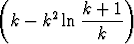 ck, k
ck, k 
 .
.
Määritä sarjan suppenemissäde ja piirrä summafunktion kuvaaja reaalialueella summeeraamalla sarjan termejä. Piirrä osasummien kuvaajia myös jonkin matkaa suppenemisalueen ulkopuolelle.
Tehtävä 93
Millä muuttujan x
 arvoilla sarja
arvoilla sarja 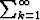 akxk suppenee, kun tiedetään, että
k < ak < k2 kaikilla indekseillä k?
akxk suppenee, kun tiedetään, että
k < ak < k2 kaikilla indekseillä k?
Tehtävä 94
Kehitä funktio
f(z) = 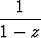
potenssisarjaksi lausekkeen z - i potenssien mukaan muokkaamalla funktion lauseke sopivan geometrisen sarjan summan muotoon. Mikä on sarjan suppenemisympyrä?
Tehtävä 95
Kehitä funktio
f(z) = 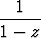
potenssisarjaksi lausekkeen z + 3 potenssien mukaan. Mikä on sarjan suppenemisympyrä?
Tehtävä 96
Muodosta origokeskinen potenssisarja funktiolle
f(z) = 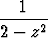 .
.
Mitä voidaan sanoa tämän suppenemisjoukosta?
Tehtävä 97
Muodosta funktion
f(z) = 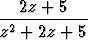
osamurtokehitelmä kompleksialueella. Tulkitse syntyneet termit lausekkeen z - 1 potenssien mukaan etenevien geometristen sarjojen summiksi ja muodosta funktion potenssisarja pisteessä z = 1. Arvioi sarjan kertoimien avulla numeerisesti suppenemissädettä. Millä reaaliakselin avoimella välillä sarja suppenee? Miten suppenemissäde suhtautuu nimittäjän nollakohtiin?
Tehtävä 98
Olkoon funktio f määritelty potenssisarjan avulla:
f(z) = 
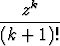 .
.
Merkitään
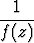 =
= 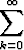
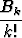 zk;
zk;
tässä B0 , B1 , B2, . . . ovat Bernoulli’n lukuja. Määritä viisi ensimmäistä Bernoulli’n lukua muodostamalla sarjojen Cauchyn tulo.
5.2 Taylorin sarja
Tehtävä 99
Olkoon
f(x) = e-1/x2
, kun x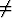 0, ja f(0) = limx
0, ja f(0) = limx 0f(x).
0f(x).
Muodosta funktion f Maclaurinin sarja.
5.3 Alkeisfunktioiden Taylorin sarjat
Tehtävä 100
Muodosta funktion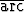 tan x Maclaurinin sarjat pisteissä x = 1 ja x = 1/
tan x Maclaurinin sarjat pisteissä x = 1 ja x = 1/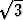 .
Todista, että nämä suppenevat ja että niiden summat ovat
.
Todista, että nämä suppenevat ja että niiden summat ovat 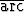 tan 1 ja
tan 1 ja 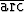 tan(1/
tan(1/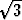 ).
Miten näiden avulla voidaan laskea luvun
).
Miten näiden avulla voidaan laskea luvun  likiarvoja? Montako termiä tarvitaan, jotta
likiarvoja? Montako termiä tarvitaan, jotta  saadaan 10 desimaalin tarkkuudella?
saadaan 10 desimaalin tarkkuudella?
Tehtävä 101
Sinifunktion arvoja lasketaan Maclaurinin sarjasta välillä [10 , 12
, 12 ]
ottamalla huomioon 60 nollasta eroavaa termiä. Arvioi tällöin syntyvää virhettä Leibnizin
testin virhearvion mukaisesti. Piirrä sinifunktion kuvaaja ja approksimaatiofunktion
kuvaaja. Havainto? Sen selitys?
]
ottamalla huomioon 60 nollasta eroavaa termiä. Arvioi tällöin syntyvää virhettä Leibnizin
testin virhearvion mukaisesti. Piirrä sinifunktion kuvaaja ja approksimaatiofunktion
kuvaaja. Havainto? Sen selitys?
Tehtävä 102
Muodosta origokeskinen potenssisarja funktiolle ln(1 + x) ja tämän avulla funktiolle
f(x) = ln 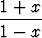 .
.
Mitkä ovat sarjojen suppenemissäteet? Minkä lukujen logaritmit jälkimmäisen sarjan avulla voidaan laskea?
Tehtävä 103
Juurelle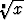 voidaan laskea likiarvoja kirjoittamalla juurrettava muotoon
x = pn + y ja kehittämällä funktio
voidaan laskea likiarvoja kirjoittamalla juurrettava muotoon
x = pn + y ja kehittämällä funktio 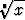 = f(y) = (pn + y)1/n binomisarjaksi. Tässä p on
sellainen luonnollinen luku, jonka n:s potenssi lähellä lukua x. Tutki approksimaatiota
tapauksessa x
= f(y) = (pn + y)1/n binomisarjaksi. Tässä p on
sellainen luonnollinen luku, jonka n:s potenssi lähellä lukua x. Tutki approksimaatiota
tapauksessa x  [15600, 15650], n = 6. Miten saavutettava tarkkuus riippuu binomisarjaan
otettavien termien lukumäärästä? Tutki erityisesti juurelle
[15600, 15650], n = 6. Miten saavutettava tarkkuus riippuu binomisarjaan
otettavien termien lukumäärästä? Tutki erityisesti juurelle 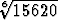 saatavia
likiarvoja.
saatavia
likiarvoja.
Tehtävä 104
Esitä binomisarjaan perustuva menettely, jolla funktio (a + bx) (a
(a 0,
b
0,
b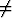 0, x
0, x 
 ) voidaan kehittää sarjaksi pisteessä x = c. Mikä on kehitelmän
suppenemisväli?
) voidaan kehittää sarjaksi pisteessä x = c. Mikä on kehitelmän
suppenemisväli?
Tehtävä 105
Muodosta origokeskiset Taylorin sarjat funktioille ez1 ja ez2. Laske näiden Cauchyn tulo ja totea, että se on lausekkeen ez1+z2 Taylorin sarja.Tehtävä 106
Esitä funktioiden ex ja e-x origokeskiset Taylorin sarjat. Muodosta näiden Cauchyn tulo. Millaisia lukuja ovat tämän kertoimet?5.4 Eri tapoja muodostaa Taylorin sarja
Tehtävä 107
Johda Maclaurinin sarja funktiolle sin 2x. Tapoja on useita; esitä ainakin kolme.Tehtävä 108
Muodosta Maclaurinin sarja funktiolle cos 2x ainakin kolmella eri tavalla.Tehtävä 109
Muodosta funktiolle ex cos x potenssisarja a) käyttäen Cauchyn tuloa, b) tarkastelemalla kompleksista eksponenttifunktiota ez.Tehtävä 110
Esitä vähintään kolme eri tapaa muodostaa funktion sin x Maclaurinin
sarja. Mikä on sarjan suppenemisympyrä kompleksitasossa?
sin x Maclaurinin
sarja. Mikä on sarjan suppenemisympyrä kompleksitasossa?
Tehtävä 111
Muodosta funktion y = tan x Maclaurinin sarja y = akxk sijoittamalla
tähän sarjaan funktion x =
akxk sijoittamalla
tähän sarjaan funktion x =  tan y Maclaurinin sarja ja vaatimalla, että tulos on
= y.
tan y Maclaurinin sarja ja vaatimalla, että tulos on
= y.
Tehtävä 112
Laske funktion ex4 kaikkien derivaattojen arvot origossa sarjakehitelmän avulla.Tehtävä 113
Etsi sellainen potenssisarja, että tämän Cauchyn tulo itsensä kanssa on

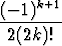 z2k.
z2k.
Mikä tunnettu trigonometrian kaava on kyseessä?
Tehtävä 114
Johda Maclaurinin sarja funktiolle f :

 ,
,
f(x) = 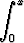 e-t2
dt.
e-t2
dt.
Millä arvoilla sarja suppenee? Laske f(1) kymmenen desimaalin tarkkuudella. Laske tulos myös integroimalla numeerisesti.
Tehtävä 115
Muodosta funktiolle f :

 ,
,
f(x) = 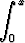
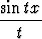 dt,
dt,
origokeskinen Taylorin sarja. Millä muuttujan x arvoilla sarja suppenee?
Tehtävä 116
Piirrä funktion
f(x) = 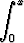
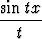 dt
dt
kuvaaja, kun x  [0, 10]. Etsi nelidesimaalinen likiarvo luvulle f(10).
[0, 10]. Etsi nelidesimaalinen likiarvo luvulle f(10).
Tehtävä 117
Laske viisidesimaalinen likiarvo integraalille
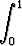
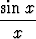 dx
dx
sarjakehitelmää käyttäen.
Tehtävä 118
Laske viisidesimaalinen likiarvo integraalille
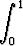
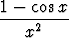 dx
dx
sarjakehitelmää käyttäen.
Tehtävä 119
Kehitä sarjaksi muuttujan x potenssien mukaan funktio
f(x) = 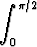
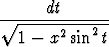 .
.
Tehtävä 120
Muodosta jonkin symbolisen tietokoneohjelman avulla funktion
f(x) = 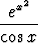
Maclaurinin sarjan osasummia. Piirrä osasumien kuvaajia ja vertaa niitä itse funktioon.
Tehtävä 121
Muodosta Maclaurinin sarjat Fresnelin integraaleille
S(x) = 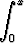 sin t2 dt, C(x) =
sin t2 dt, C(x) = 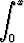 cos t2 dt.
cos t2 dt.
Millä muuttujan x arvoilla nämä sarjat suppenevat?
Tehtävä 122
Muodosta astetta 10 olevat Taylorin polynomit funktiolle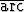 sin x pisteissä
x = 0 ja x =
sin x pisteissä
x = 0 ja x =  . Piirrä funktion ja polynomien kuvaajat.
. Piirrä funktion ja polynomien kuvaajat.