13 Erityyppisten integraalien väliset yhteydet
13.1 Gaussin lause
Tehtävä 364
Laske
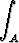
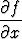 da,
da,
kun A on tason origokeskinen yksikköympyrä, jonka kehällä funktion f arvot saadaan lausekkeesta f(x, y) = 2x - 3y2.
Tehtävä 365
Tarkista laskemalla Greenin lauseen voimassaolo, kun u(x, y) = (2xy - x2)i + (x + y2)j ja integroidaan käyrien y = x2 ja x = y2 rajaaman rajoitetun alueen yli.Tehtävä 366
Laske integraali
 (ex - 4y sin 2x)dx + (2x + sin 2x)dy
(ex - 4y sin 2x)dx + (2x + sin 2x)dy
a) suoraan viivaintegraalina, b) palauttamalla tasointegraaliksi. Tie c on neliön
{ (x, y) | |x| < 2, |y| < 2 }
piiri positiiviseen suuntaan kierrettynä.
Tehtävä 367
Laske a) suoraan viivaintegraalina, b) tasointegraaliksi muuntamalla
 y2 dx + (x + y)2 dy,
y2 dx + (x + y)2 dy,
kun c on sen kolmion piiri positiiviseen suuntaan kierrettynä, jonka kärjet ovat (a, 0), (a, a) ja (0, a); oletetaan a > 0.
Tehtävä 368
Olkoon funktio f(x) jatkuvasti derivoituva ja olkoon u(x, y) = (2xy - y) i + f(x) j tason vektorikenttä. Olkoon c säännöllinen umpinainen tasokäyrä. Osoita, että f voidaan valita äärettömän monella tavalla siten, että integraali u . dr antaa käyrän c
reunustaman alueen pinta-alan.
u . dr antaa käyrän c
reunustaman alueen pinta-alan.
Tehtävä 369
Laske
 u . dn,
u . dn,
kun u(x, y) = (x + ey)i + (sin x + 2y)j, tie c on ellipsi x2/a2 + y2/b2 = 1 positiiviseen suuntaan kierrettynä ja n on tämän yksikköulkonormaalivektori. Tehtävä voidaan laskea joko suoraan viivaintegraalina tai palauttamalla tasointegraaliksi.
Tehtävä 370
Olkoon A tasoalue ja A tämän reuna, joka oletetaan säännölliseksi
käyräksi. Funktio u(x, y) olkoon harmoninen, ts.
A tämän reuna, joka oletetaan säännölliseksi
käyräksi. Funktio u(x, y) olkoon harmoninen, ts.  2u = 0 alueessa A. Osoita,
että
2u = 0 alueessa A. Osoita,
että

 ds = 0,
ds = 0,
missä  tarkoittaa funktion u derivaattaa reunan
tarkoittaa funktion u derivaattaa reunan  A ulkonormaalin suuntaan.
A ulkonormaalin suuntaan.
Tehtävä 371
Laske vektorikentän u(x, y, z) = xi + y2j - k vuo kuution{ (x, y, z) | |x| < 1, |y| < 1, |z| < 1 }
pinnan läpi a) pintaintegraalina, b) avaruusintegraalina.
Tehtävä 372
Laske vektorikentän u(x, y, z) = z2(x i + y j) + k vuo kuution |x| < , |y| <
, |y| <  , |z| <
, |z| <  pinnan läpi.
pinnan läpi.
Tehtävä 373
Laske Gaussin lauseen avulla kentän u(x, y, z) = x2 i + y2 j + z2 k vuo kuution { (x, y, z) | |x| < 1, |y| < 1, |z| < 1 } pinnan läpi.Tehtävä 374
Laske Gaussin lauseen avulla kentän u(x, y, z) = ex cos y i + ecos z j + ex sin y k vuo kuution { (x, y, z) | |x| < 1, |y| < 1, |z| < 1 } pinnan läpi.Tehtävä 375
Olkoon V koordinaattitasojen ja tason x + y + z = 1 rajoittama alue, V
tämän reunapinta. Olkoon u(x, y, z) = 2xyi + 3yj + 2zk. Laske Gaussin lausetta käyttäen
integraali
V
tämän reunapinta. Olkoon u(x, y, z) = 2xyi + 3yj + 2zk. Laske Gaussin lausetta käyttäen
integraali
 u . dS.
u . dS.
Tehtävä 376
Laske vektorikentän u(x, y, z) = (x2 - 1) i - x2y j + z2 k vuo pintojen z = 0, z = 1 ja x2 + y2 = 4 rajoittaman kappaleen pinnan läpi.Tehtävä 377
Laske vektorikentän u(x, y, z) = x4 i + y2z2 j + z k vuo kappaleen { (x, y, z) | x2 + y2 < 1, 0 < z < 1 } pinnan läpi.Tehtävä 378
Laske vuo
 (x i - y j + z k) . dS,
(x i - y j + z k) . dS,
kun V = { (x, y, z) | x2 + y2 + z2 - 4y + 2z + 2 < 0 }.
Tehtävä 379
Määritä pintaintegraalin
 [(x + y) i - 2xz j + (y - z) k] × dS
[(x + y) i - 2xz j + (y - z) k] × dS
arvo, kun integroimisjoukkona on palloneljänneksen { (x, y, z) | x2 + y2 + z2 < 1, x > 0, y > 0 } pinta.
Tehtävä 380
Olkoon A rajoitettu tason 2 alue ja V vastaavasti rajoitettu avaruuden
2 alue ja V vastaavasti rajoitettu avaruuden  3
alue; näiden reunat
3
alue; näiden reunat  A ja
A ja  V olkoot säännöllisiä. Mikä geometrinen merkitys on
seuraavilla integraaleilla:
V olkoot säännöllisiä. Mikä geometrinen merkitys on
seuraavilla integraaleilla:
a) 
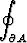 r . dn, b)
r . dn, b) 
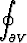 r . dS ?
r . dS ?
Tehtävä 381
Vektorikenttä u olkoon rajoitetun alueen V säännöllisellä pinnalla kaikkialla kohtisuorassa pintaa vastaan. Osoita, että

 × u dv = o.
× u dv = o.
Tehtävä 382
Osoita:
 r dv =
r dv = 
 r2 dS.
r2 dS.
Tehtävä 383
Olkoon V alue, jolla on säännöllinen pinta V ; olkoon origo alueen V
ulkopiste. Muunna seuraavat pintaintegraalit alueen V yli otetuiksi avaruusintegraaleiksi:
V ; olkoon origo alueen V
ulkopiste. Muunna seuraavat pintaintegraalit alueen V yli otetuiksi avaruusintegraaleiksi:
a) 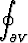
 dS, b)
dS, b) 
 dS.
dS.
Tehtävä 384
Olkoon c vakiovektori. Laske
 (c × r) × dS.
(c × r) × dS.
Tehtävä 385
Skalaarikenttä u(x, y, z) olkoon kahdesti jatkuvasti derivoituva avaruuden 3
säännöllisessä rajoitetussa joukossa V . Osoita:
3
säännöllisessä rajoitetussa joukossa V . Osoita:

 dS =
dS = 
 2u dv,
2u dv,
missä 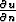 tarkoittaa funktion u suunnattua derivaattaa pinnan
tarkoittaa funktion u suunnattua derivaattaa pinnan  V ulkonormaalin
suuntaan.
V ulkonormaalin
suuntaan.
Tehtävä 386
Olkoot u ja v kahdesti jatkuvasti derivoituvia funktioita 3
3 
 sekä V alue, jonka reuna
sekä V alue, jonka reuna  V on säännöllinen. Oletetaan lisäksi, että
V on säännöllinen. Oletetaan lisäksi, että  v on
jokaisessa reunan
v on
jokaisessa reunan  V pisteessä tangenttitason suuntainen. Laske Gaussin lauseen
avulla
V pisteessä tangenttitason suuntainen. Laske Gaussin lauseen
avulla
 (u
(u 2v +
2v +  u .
u .  v)dv.
v)dv.
Tehtävä 387
Olkoon u : 3
3 
 jatkuvasti derivoituva funktio, jonka tasa-arvopinnat
ovat umpinaisia säännöllisisä pintoja siten, että pienempää arvoa vastaava pinta aina jää
suurempaa arvoa vastaavan sisään. Mikä geometrinen tulkinta on tietyn tasa-arvopinnan
rajoittaman alueen V yli otetun integraalin
jatkuvasti derivoituva funktio, jonka tasa-arvopinnat
ovat umpinaisia säännöllisisä pintoja siten, että pienempää arvoa vastaava pinta aina jää
suurempaa arvoa vastaavan sisään. Mikä geometrinen tulkinta on tietyn tasa-arvopinnan
rajoittaman alueen V yli otetun integraalin

 .
. 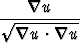 dv
dv
arvolla?
Tehtävä 388
Olkoon V
 3 rajoitettu joukko, jolla on origo sisäpisteenä ja jonka reuna
3 rajoitettu joukko, jolla on origo sisäpisteenä ja jonka reuna
 V on säännöllinen. Laske
V on säännöllinen. Laske
| a) epäoleellinen avaruusintegraali | 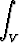  . .   dv, dv, | ||||||
| b) pintaintegraali |    . dS. . dS. |
Seuraako Gaussin lauseesta, että integraalien arvot ovat samat?
Tehtävä 389
Laske avaruuden 3 vektorikentän u(r) = r/r3 vuo origokeskisen R-säteisen
pallopinnan läpi. Laske kentän divergenssi. Voidaanko vuo laskea Gaussin lauseen avulla?
Jos ei, niin miksi ei?
3 vektorikentän u(r) = r/r3 vuo origokeskisen R-säteisen
pallopinnan läpi. Laske kentän divergenssi. Voidaanko vuo laskea Gaussin lauseen avulla?
Jos ei, niin miksi ei?
Tehtävä 390
Laske vektorikentän u(r) = rr (r paikkavektori, r sen pituus) vuo R-säteisen origokeskisen pallon läpi a) pintaintegraalina, b) muuntamalla pintaintegraali Gaussin lauseen avulla avaruusintegraaliksi. Millainen on kentän u lähdekenttä xyz-koordinaateissa?Tehtävä 391
Osoita Gaussin lauseen avulla, että pintaintegraali

 r . dS
r . dS
on riippumaton siitä, millainen origoa ympäröivä (säännöllinen) pinta S on. (Tässä r on paikkavektori ja r sen itseisarvo.) Laske integraali valitsemalla pinnaksi S origokeskinen pallopinta.
Tehtävä 392
Homogeenisessa nesteessä vallitsee syvyydessä z paine p = p0 + g z, missä g
on maan vetovoiman kiihtyvyys,
z, missä g
on maan vetovoiman kiihtyvyys,  nesteen tiheys ja p0 paine nesteen pinnalla.
Nesteeseen upotetun kappaleen pinta-alkioon dS vaikuttaa tällöin voima -pn dS;
kokonaisvoima saadaan integroimalla tämä lauseke kappaleen pinnan yli. Sovella
tähän integraaliin yleistettyä Gaussin lausetta ja johda tällä tavoin Arkhimedeen
periaate.
nesteen tiheys ja p0 paine nesteen pinnalla.
Nesteeseen upotetun kappaleen pinta-alkioon dS vaikuttaa tällöin voima -pn dS;
kokonaisvoima saadaan integroimalla tämä lauseke kappaleen pinnan yli. Sovella
tähän integraaliin yleistettyä Gaussin lausetta ja johda tällä tavoin Arkhimedeen
periaate.
13.2 Stokesin lause
Tehtävä 393
Olkoon c on puoliympyrän { (x, y) | x2 + y2 < 1, x > 0 } piiri. Laske viivaintegraali
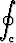 (x + y2) dr
(x + y2) dr
a) suoraan viivaintegraalina, b) muuntamalla se ensin sopivaa Stokesin lauseen muotoa käyttäen.
Tehtävä 394
Laske suoraan viivaintegraalina ja Stokesin lauseen avulla
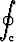 (z i + x j + y k) . dr,
(z i + x j + y k) . dr,
kun c on lieriön x2 + y2 = 9 ja tason 3x + 2y + z = 6 leikkauskäyrä kierrettynä origosta katsottaessa vastapäivään.
Tehtävä 395
Laske sekä suoraan viivaintegraalina että Stokesin lauseen avulla

![[yz i + (xz2 - 3y) j- xyk]](kuvat/va509x.gif) . dr,
. dr,
missä c on käyrä r(t) = cos t i + sin t j + cos t k, t  [0, 2
[0, 2 ].
].
Tehtävä 396
Olkoon u(x, y, z) = yzexy i + xz(1 + exy) j + exy k. Laske viivaintegraali
 u . dr,
u . dr,
missä c on lieriön x2 + y2 = 4 ja tason 2x + 3y + z = 5 leikkauskäyrä kierrettynä origosta katsottaessa myötäpäivään.
Tehtävä 397
Laske vektorikentän u(x, y, z) = x k viivaintegraali u . dr, kun c on
pinnanpalan
u . dr, kun c on
pinnanpalan
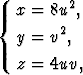 0 < u < 1, 0 < v < 3
0 < u < 1, 0 < v < 3
reuna a) suoraan viivaintegraalina, b) muuntamalla integraali ensin Stokesin lauseen avulla pintaintegraaliksi.
Tehtävä 398
Laske integraali
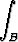
 × (k × r) . dS,
× (k × r) . dS,
kun B on a) xy-tason yksikkökiekko { (x, y, 0) | x2 + y2 < 1 }, b) avaruuden  3
yksikköpallon { (x, y, z) | x2 + y2 + z2 = 1 } ylempi puolipallo, c) em. yksikköpallon alempi
puolipallo. Pinta-alkioon dS sisältyvä normaalisuunta otetaan a-kohdassa ylöspäin, b- ja
c-kohdissa pallosta ulospäin.
3
yksikköpallon { (x, y, z) | x2 + y2 + z2 = 1 } ylempi puolipallo, c) em. yksikköpallon alempi
puolipallo. Pinta-alkioon dS sisältyvä normaalisuunta otetaan a-kohdassa ylöspäin, b- ja
c-kohdissa pallosta ulospäin.
Tehtävä 399
Olkoon u(x, y, z) = z i + x j + y k vektorikenttä ja z = xy, |x| < 1, |y| < 1 pinnanapala. Laske viivaintegraali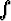 u . dr pitkin pinnanpalan reunaa a) suoraan
viivaintegraalina, b) muuntamalla se ensin pintaintegraaliksi Stokesin lauseen
avulla.
u . dr pitkin pinnanpalan reunaa a) suoraan
viivaintegraalina, b) muuntamalla se ensin pintaintegraaliksi Stokesin lauseen
avulla.
Tehtävä 400
Laske Stokesin lauseen avulla pintaintegraali
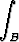
 × [(x - z2) i + (x3 + z) j + xy k] . dS,
× [(x - z2) i + (x3 + z) j + xy k] . dS,
missä B on huipun ja xy-tason väliin jäävä kartiopinnan x2 + y2 = (z - 1)2 osa. Häiritseekö kartion huippu Stokesin lauseen käyttöä?
Tehtävä 401
Osoita:
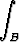 dS × r =
dS × r = 
 r2 dr,
r2 dr,
missä B on jokin säännöllinen pinnanpala ja 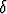 B sen reuna pinnan normaaliin nähden
positiiviseen suuntaan kierrettynä.
B sen reuna pinnan normaaliin nähden
positiiviseen suuntaan kierrettynä.
Tehtävä 402
Olkoon c vakiovektori, B jokin säännöllinen pinnanpala ja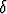 B sen
reuna pinnan normaaliin nähden positiiviseen suuntaan kierrettynä. Osoita,
että
B sen
reuna pinnan normaaliin nähden positiiviseen suuntaan kierrettynä. Osoita,
että
a)  c . dS = c . c . dS = c .  dS = dS =   c × r . dr; c × r . dr; | |||
b)  c × dS = c × c × dS = c × 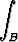 dS = - dS = - r × (dr × c). r × (dr × c). |
13.3 Gaussin ja Stokesin lauseen yleistyksiä
Tehtävä 403
Olkoon u : 3
3 
 harmoninen funktio ja V
harmoninen funktio ja V 
 3 rajoitettu joukko, jonka
reuna
3 rajoitettu joukko, jonka
reuna  V on säännöllinen. Osoita:
V on säännöllinen. Osoita:
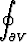 u
u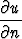 dS =
dS =  |
| u|2 dv.
u|2 dv.
Tässä 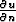 on funktion u derivaatta pinnan
on funktion u derivaatta pinnan  V ulkonormaalin suuntaan.
V ulkonormaalin suuntaan.
13.4 Kulma ja avaruuskulma
Tehtävä 404
Neliön kärjet sijaitsevat pisteissä (1, 1, 1), (1, 0, 1), (1, 0, 0) ja (1, 1, 0). Kirjoita integraali, joka esittää sen avaruuskulman suuruutta, jossa neliö näkyy origosta.Tehtävä 405
Laske edellisen tehtävän integraali tai sen likiarvo seuraavilla tavoilla: a) geometrinen päättely, b) integrointi kynällä ja paperilla, c) symbolinen tietokoneohjelma.Tehtävä 406
Neliön kärjet sijaitsevat pisteissä (a, -1, -1), (a, 1, -1), (a, 1, 1) ja (a, -1, 1), a > 0. Muodosta integraali, joka esittää sen avaruuskulman suuruutta, jossa neliö näkyy origosta. Laske integraali. Mikä on avaruuskulman raja-arvo, kun a 0?
0?